An approximate analytical solution of the Bethe equation for charged particles in the radiotherapeutic energy range

Abstract

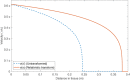
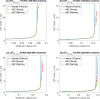
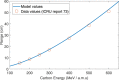
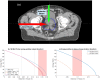
Charged particles such as protons and carbon ions are an increasingly important tool in radiotherapy. There are however unresolved physics issues impeding optimal implementation, including estimation of dose deposition in non-homogeneous tissue, an essential aspect of treatment optimization. Monte Carlo (MC) methods can be employed to estimate radiation profile, and whilst powerful, these are computationally expensive, limiting practicality. In this work, we start from fundamental physics in the form of the Bethe equation to yield a novel approximate analytical solution for particle range, energy and linear energy transfer (LET). The solution is given in terms of the exponential integral function with relativistic co-ordinate transform, allowing application at radiotherapeutic energy levels (50-350 MeV protons, 100-600 Mev/a.m.u carbon ions). Model results agreed closely for protons and carbon-ions (mean error within ≈1%) of literature values. Agreement was high along particle track, with some discrepancy manifesting at track-end. The model presented has applications within a charged particle radiotherapy optimization framework as a rapid method for dose and LET estimation, capable of accounting for heterogeneity in electron density and ionization potential.

Figure 1

Comparison of v(x′) and v(x) (note Velocity shown on the vertical axis as a fraction of the speed of light c) for a 250 MeV proton. In this example, the projected range of the proton is 38.15 cm when the relativistic transform is considered. If this were neglected, projected range would be only 24.36 cm. This substantial difference suggests that taking account of the relativistic transform is vital for particles in the radiotherapy energy range.

Figure 2

Comparison of model with numerical solution of the full Bethe equation (Equation 1) and the simplified form (Equation 6) for (a) a high energy proton and (b) a high energy Carbon ion. High energies are shown here as this is where maximum disagreement should manifest. As can be seen from the figure, the model matches the numerical solutions to a very high degree of accuracy, even at these high energies.

Figure 3

Comparison of pristine (mono-energetic) model predictions and MC simulations for proton mean energy as a function of depth, for protons with initial energies of 100–250 MeV in both broad and narrow cross section phantoms.

Figure 4

Comparison of pristine (mono-energetic) model predictions and and MC simulations for proton unrestricted LET as a function of depth, for protons with with initial energies of 100–250 MeV in both broad and narrow cross section phantoms.

Figure 5

Comparison of tabulated range data for Carbon-ions from ICRU report 73 versus model predictions. High agreement was found along the full energy range, with R ² = 0.9968 between model and data.

Figure 6

(a) Typical radiotherapy treatment planning scan for prostate cancer, with tumour volume outlined in blue. Possible anterior and lateral beam trajectories are indicated with arrows. A lateral beam passes through 7.3 cm of tissue before encountering 5.6 cm of bone and finally the organ. The anterior beam passes through a more uniform medium. (b) Energy profiles for 160 MeV protons, assuming different constituent tissues along the lateral beam trajectory. Regions of tumour are denoted by the shaded area and tissue interfaces by the vertical dashed lines (c) Energy profiles for protons entering along the anterior beam trajectory, with tumour region shaded. In this case, a 160 MeV proton would deposit the bulk of its energy downstream of the tumour into radio-sensitive tissue. By contrast, lower energy protons such as the 100 MeV path shown here would be sufficient to target the tumour volume.

Figure 7

Energy profile for a 250 MeV proton in water with different choices of mean ionization potential, I, shown between 0.3 ≤ x ≤ R _T. Profiles are initially similar, with divergence manifesting towards path end.

Figure 8

Example proton Bragg curves in water, found using calculations of proton kinetic energy as a function of path length from this work, combined with published formulations for energy and range straggling.