Entropy spikes as a signature of Lifshitz transitions in the Dirac materials

Abstract

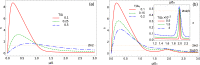
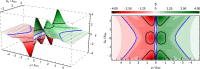
We demonstrate theoretically that the characteristic feature of a 2D system undergoing N consequent Lifshitz topological transitions is the occurrence of spikes of entropy per particle s of a magnitude ±ln2/(J - 1/2) with 2 ≤ J ≤ N at low temperatures. We derive a general expression for s as a function of chemical potential, temperature and gap magnitude for the gapped Dirac materials. Inside the smallest gap, the dependence of s on the chemical potential exhibits a dip-and-peak structure in the temperature vicinity of the Dirac point. The spikes of the entropy per particles can be considered as a signature of the Dirac materials. These distinctive characteristics of gapped Dirac materials can be detected in transport experiments where the temperature is modulated in gated structures.

Figure 1

The entropy per electron s vs the chemical potential μ > 0, s(−μ) = −s(μ), for three values of temperature. Left panel: (a): Gapped graphene. The chemical potential μ is expressed in the units of Δ; the solid (red) T/Δ = 0.1, dashed (green) T/Δ = 0.25, dash-dotted (blue) T/Δ = 0.5. Right panel: (b): Silicene. μ is in the units of a smaller gap Δ₁, the second gap Δ₂ = 2Δ₁; the solid (red) T/Δ₁ = 0.1, dashed (green) T/Δ₁ = 0.15, dash-dotted (blue) T/Δ₁ = 0.2. The vicinity of μ = Δ₂ is shown in the insert: the solid (red) T/Δ₁ = 5 × 10⁻³, dashed (green) T/Δ₁ = 1.5 × 10⁻², dash-dotted (blue) T/Δ₁ = 3 × 10⁻².

Figure 2

The entropy per electron s as functions of the chemical potential μ and temperature T in the units of Δ₁. The gap Δ₂ = 4Δ₁. Left panel: 3D plot. Right panel: Contour plot.

Figure 3

The entropy per electron s as functions of the chemical potential μ and Δ_z in the units of Δ_SO. The temperature T = 0.3Δ_SO. Left panel: 3D plot. Right panel: Contour plot.