Monte Carlo simulation-based estimation for the minimum mortality temperature in temperature-mortality association study

Abstract

Background: Rich literature has reported that there exists a nonlinear association between temperature and mortality. One important feature in the temperature-mortality association is the minimum mortality temperature (MMT). The commonly used approach for estimating the MMT is to determine the MMT as the temperature at which mortality is minimized in the estimated temperature-mortality association curve. Also, an approximate bootstrap approach was proposed to calculate the standard errors and the confidence interval for the MMT. However, the statistical properties of these methods were not fully studied.

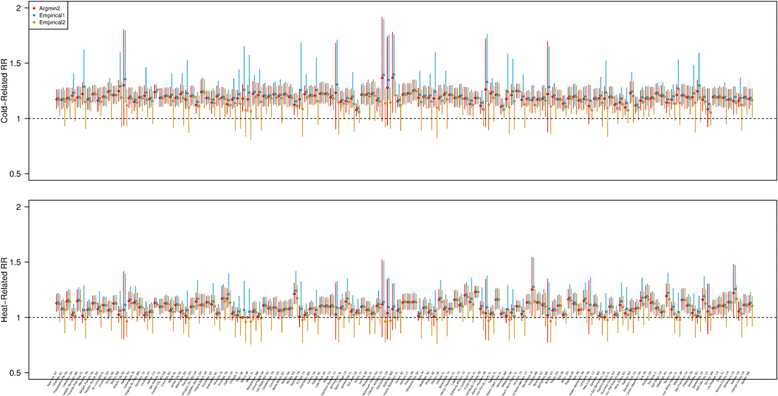
Methods: Our research assessed the statistical properties of the previously proposed methods in various types of the temperature-mortality association. We also suggested an alternative approach to provide a point and an interval estimates for the MMT, which improve upon the previous approach if some prior knowledge is available on the MMT. We compare the previous and alternative methods through a simulation study and an application. In addition, as the MMT is often used as a reference temperature to calculate the cold- and heat-related relative risk (RR), we examined how the uncertainty in the MMT affects the estimation of the RRs.

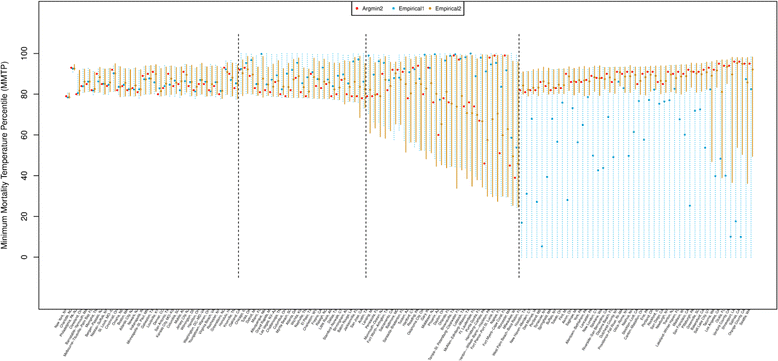
Results: The previously proposed method of estimating the MMT as a point (indicated as Argmin2) may increase bias or mean squared error in some types of temperature-mortality association. The approximate bootstrap method to calculate the confidence interval (indicated as Empirical1) performs properly achieving near 95% coverage but the length can be unnecessarily extremely large in some types of the association. We showed that an alternative approach (indicated as Empirical2), which can be applied if some prior knowledge is available on the MMT, works better reducing the bias and the mean squared error in point estimation and achieving near 95% coverage while shortening the length of the interval estimates.

Conclusions: The Monte Carlo simulation-based approach to estimate the MMT either as a point or as an interval was shown to perform well particularly when some prior knowledge is incorporated to reduce the uncertainty. The MMT uncertainty also can affect the estimation for the MMT-referenced RR and ignoring the MMT uncertainty in the RR estimation may lead to invalid results with respect to the bias in point estimation and the coverage in interval estimation.

Keywords: Minimum mortality temperature; Monte Carlo simulation-based estimation; Point and interval estimation.

Fig. 1

Estimated minimum mortality temperature (MMT) percentile for 135 cities in the US by three different methods; Argmin2 (red), Empirical1 (blue), Empirical2_minimal (orange). Points indicate the point estimate and vertical solid/dashed bars indicate 95% empirical interval estimates. Cities are ordered according to the MMT uncertainty (the length of the interval estimates obtained by Empirical1). The cities are divided into 4 categories (indicated by black dashed vertical lines) with respect to the MMT uncertainty and temperature-mortality association types (refer to Fig. S8)

Fig. 2

Estimated cold- and heat- related relative risk (RR) for 135 cities in the US by three different methods; Argmin2 (red), Empirical1 (blue), Empirical2_minimal (orange). Points indicate the point estimate and vertical solid/dashed bars indicate 95% empirical interval estimates. Cities are ordered according to the MMT uncertainty (the length of the interval estimates obtained by Empirical1) as in Fig. 1