Time-Dependent Material Properties of Shotcrete: Experimental and Numerical Study

Abstract

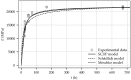
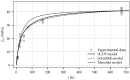
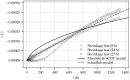
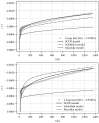
A new experimental program, focusing on the evolution of the Young's modulus, uniaxial compressive strength, shrinkage and creep of shotcrete is presented. The laboratory tests are, starting at very young ages of the material, conducted on two different types of specimens sampled at the site of the Brenner Basetunnel. The experimental results are evaluated and compared to other experiments from the literature. In addition, three advanced constitutive models for shotcrete, i.e., the model by Meschke, the model by Schädlich and Schweiger, and the model by Neuner et al., are validated on the basis of the test data, and the capabilities of the models to represent the observed shotcrete behavior are assessed. Hence, the gap between the the outdated experimental data on shotcrete available in the literature on the one hand and the nowadays available advanced shotcrete models, on the other hand, is closed.

Keywords: constitutive model; creep; damage model; material tests; plasticity model; shotcrete; shrinkage; sprayed concrete.

Figure 1

Molds for sprayed specimens: slotted tubes, fixed with a clamp on the upper side and mounted on a wooden rig.

Figure 2

Sealed specimen in the creep test bench with displacement transducers fixed to the specimen.

Figure 3

Evolution of the Young’s modulus: experimental results from the present experimental program and test data by Müller.

Figure 4

Evolution of the uniaxial compressive strength: experimental results from the present experimental program and test data by Müller.

Figure 5

Mean values and standard deviations (SD) of the Young’s modulus and the uniaxial compressive strength for the present experimental program.

Figure 6

Evolution of the total strain determined on sealed, load-free specimens: experimental results for the tests on three specimens of the present experimental program, started at shotcrete ages of 8 h, 24 h and 27 h.

Figure 7

Evolution of the total strain determined on sealed, loaded specimens: experimental results for the tests on three specimens of the present experimental program, started at shotcrete ages of 8 h, 24 h and 27 h.

Figure 8

Compliance functions determined from the creep tests of the present experimental program, started at shotcrete ages of 8 h, 24 h and 27 h, and compliance functions from creep test series 4/2, conducted on two specimens by Müller, started at the shotcrete age of 48 h.

Figure 9

Evolution of the Young’s modulus: experimental results and computed numerical results based on the calibrated shotcrete models.

Figure 10

Evolution of the uniaxial compressive strength: experimental results and computed numerical results based on the calibrated shotcrete models.

Figure 11

Evolution of the total strain determined on sealed, load-free specimens: experimental results and computed numerical results based on the calibrated shotcrete models.

Figure 12

Evolution of the total strain determined on sealed, loaded specimens: Experimental results from the creep tests started at shotcrete ages of 8 h (top), 24 h (middle) and 27 h (bottom) and the respective computed numerical results based on the calibrated shotcrete models.

Figure 12

Evolution of the total strain determined on sealed, loaded specimens: Experimental results from the creep tests started at shotcrete ages of 8 h (top), 24 h (middle) and 27 h (bottom) and the respective computed numerical results based on the calibrated shotcrete models.