Nonuniqueness in dual-energy CT

Abstract

Purpose: The goal is to determine whether dual-energy computed tomography (CT) leads to a unique reconstruction using two basis materials.

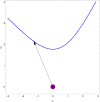
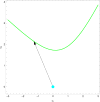
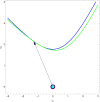
Methods: The beam-hardening equation is simplified to the single-voxel case. The simplified equation is rewritten to show that the solution can be considered to be linear operations in a vector space followed by a measurement model which is the sum of the exponential of the coordinates. The case of finding the concentrations of two materials from measurements of two spectra with three photon energies is the simplest non-trivial case and is considered in detail.

Results: Using a material basis of water and bone, with photon energies of 30 keV, 60 keV, and 100 keV, a case with two solutions is demonstrated.

Conclusions: Dual-energy reconstruction using two materials is not unique as shown by an example. Algorithms for dual-energy, dual-material reconstructions need to be aware of this potential ambiguity in the solution.

Keywords: dual-energy CT; nonuniqueness; proof by example.

FIG. 1

Graphical representation of objects in the log spectrum space. Each axis labeled s_E for E = 1, 2, 3, represents a component in the log-spectrum space. The purple dot represents the initial spectrum; technically, it is a point representing the log of the source-detector product. Symbolically, the purple dot represents s_jE in Eq. (3) for a particular j and all E. The black arrow represents effect of attenuation by the material on the spectrum, symbolically $-{\displaystyle {\sum }_i{f}_i{\alpha }_{iE}}$. It is the vector sum of the blue arrow representing the attenuation −f₁α_1E, due to the first material, water, and the brown arrow representing the attenuation −f₂α_2E due to the second material, bone. The tip of the black arrow is located at $s_{jE}-{\displaystyle {\sum }_i{f}_i{\alpha }_{iE}}$. The two-dimensional subspace spanned by the attenuation due to the two materials including the initial spectrum is shown in the lavender plane. The light brown surface, which includes the point at the tip of the black arrow, represents the isosurface to which a particular measurement, i.e., a particular value of I_j, constrains the solution to lie in.

FIG. 2

The c₁, c₂ plane is a linear transformation of the light blue plane shown in Fig. 1. The purple dot and the black arrow are defined in Fig. 1. The blue curve is the intersection of the lavender and brown surface in Fig. 1, transformed to the c₁, c₂ coordinates.

FIG. 3

The cyan dot represents a second spectrum-detector product and is analogous to the purple dot in Fig. 1. The black arrow is the same vector as in Fig. 1. The pink surface and the light green plane are analogous to the light brown surface and the lavender plane in Fig. 1, respectively.

FIG. 4

The cyan dot and green curves are analogous to the purple dot and blue curve of Fig. 2. The black arrow is the same vector as in Fig. 2.

FIG. 5

Figs. 2 and 4 are superposed. The purple and cyan dots are co-located at the origin. The black arrow points to the intersection of the two curves. This point is at the expected solution, by construction.

FIG. 6

A blow-up of the c₁-c₂ plane, the material plane in a transformed variable. The solid circle is centered at the expected solution. The dashed circle is centered at a second solution.