Stability of hand force production. I. Hand level control variables and multifinger synergies

Abstract

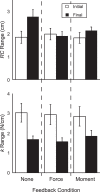
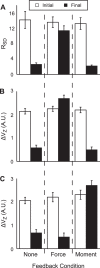
We combined the theory of neural control of movement with referent coordinates and the uncontrolled manifold hypothesis to explore synergies stabilizing the hand action in accurate four-finger pressing tasks. In particular, we tested a hypothesis on two classes of synergies, those among the four fingers and those within a pair of control variables, stabilizing hand action under visual feedback and disappearing without visual feedback. Subjects performed four-finger total force and moment production tasks under visual feedback; the feedback was later partially or completely removed. The "inverse piano" device was used to lift and lower the fingers smoothly at the beginning and at the end of each trial. These data were used to compute pairs of hypothetical control variables. Intertrial analysis of variance within the finger force space was used to quantify multifinger synergies stabilizing both force and moment. A data permutation method was used to quantify synergies among control variables. Under visual feedback, synergies in the spaces of finger forces and hypothetical control variables were found to stabilize total force. Without visual feedback, the subjects showed a force drift to lower magnitudes and a moment drift toward pronation. This was accompanied by disappearance of the four-finger synergies and strong attenuation of the control variable synergies. The indexes of the two types of synergies correlated with each other. The findings are interpreted within the scheme with multiple levels of abundant variables.NEW & NOTEWORTHY We extended the idea of hierarchical control with referent spatial coordinates for the effectors and explored two types of synergies stabilizing multifinger force production tasks. We observed synergies among finger forces and synergies between hypothetical control variables that stabilized performance under visual feedback but failed to stabilize it after visual feedback had been removed. Indexes of two types of synergies correlated with each other. The data suggest the existence of multiple mechanisms stabilizing motor actions.

Keywords: multifinger coordination; referent coordination; synergy; uncontrolled manifold hypothesis.

Fig. 1.

Schematic of the sensor motion during the experimental trials (top) and illustration of the inverse piano apparatus (bottom). On the sensor motion illustration, the vertical broken line represents the time at which visual feedback was removed (8 s after trial onset), whereas the two shaded areas indicate the times over which response variables were computed for initial and final comparisons. The inverses piano apparatus is shown with all four fingers raised by means of linear actuators, which are mounted under the table and therefore not visible in the illustration.

Fig. 2.

Across-subjects average force (F_TOT) and moment (M_TOT) production performance. Large deviations at 5 and 19.5 s result from fingers being lifted to measure referent coordinate (RC) and apparent stiffness (k) values. Visual feedback was removed at 8 s after trial onset (vertical broken line). Note the drifts in performance variables (F_TOT and M_TOT) when feedback on that variable was removed. Error shades show SE.

Fig. 3.

The {RC; k} values from a representative subject for each trial during initial (open triangles) and final (gray circles) time points, before and after, respectively, visual feedback was removed in the three visual feedback conditions: no feedback, force feedback, and moment feedback. R² values refer to best-fit hyperbolas computed for initial (solid line) and final (broken line) {RC; k} datasets.

Fig. 4.

Average values of RC (A) and k (B) for each feedback condition before (open bars) and after (filled bars) performance drifts occurred, as well as average within-trial changes in RC (C) and k (D) during these drifts. Error bars are SE.

Fig. 5.

Average values of the ranges of RC (top) and k (bottom) during full visual feedback (open bars) and partial or no visual feedback (filled bars) for different feedback conditions. Error bars are SE.

Fig. 6.

A: results of permutation analysis quantifying F_TOT-stabilizing covariation of {RC; k} values, R_SD. R_SD is the ratio of SD of force produced by permuted datasets to force produced in experimental trials. B and C: uncontrolled manifold (UCM)-based ANOVA with respect to F_TOT (B) and M_TOT (C): ΔV_Z is the z-transformed ∆V index. Error bars are SE.

Fig. 7.

Z-transformed synergy index, ΔV_Z, plotted against R_SD for all subjects. Each subject contributes 6 values of R_SD and ΔV_Z to the plot measured before and after feedback was removed across the three feedback conditions.

Fig. 8.

Schematic of force-coordinate characteristics for the agonist and antagonist muscle groups (curved broken lines) and for the effector (fingertip, straight solid lines). The neural control of the system may be described with changes in activation thresholds for the opposing muscle groups [activation thresholds for agonist (λ_ag) and antagonist (λ_ant)]. The c-command defines the spatial range where both muscle groups are active. Force production in isometric conditions [actual coordinate (AC)] is shown with black filled circles. If the c-command is large (A), both muscles are active, and the force-coordinate characteristic is close to linear. If the c-command is small (C), only agonist muscles are active, and the force-coordinate characteristic is nonlinear. In both cases, a drift in the c-command (B and D) results in a force drop, a drop in the slope (k) of the tangential line to the force-coordinate characteristic, with or without a change in the referent effector coordinate (RC, midpoint between λ_ag and λ_ant).