What Can Be Learned from Nuclear Resonance Vibrational Spectroscopy: Vibrational Dynamics and Hemes

Abstract

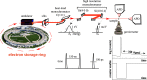
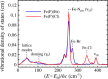
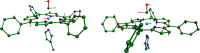
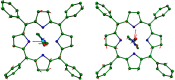
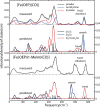
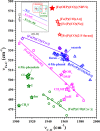
Nuclear resonance vibrational spectroscopy (NRVS; also known as nuclear inelastic scattering, NIS) is a synchrotron-based method that reveals the full spectrum of vibrational dynamics for Mössbauer nuclei. Another major advantage, in addition to its completeness (no arbitrary optical selection rules), is the unique selectivity of NRVS. The basics of this recently developed technique are first introduced with descriptions of the experimental requirements and data analysis including the details of mode assignments. We discuss the use of NRVS to probe ⁵⁷Fe at the center of heme and heme protein derivatives yielding the vibrational density of states for the iron. The application to derivatives with diatomic ligands (O₂, NO, CO, CN^-) shows the strong capabilities of identifying mode character. The availability of the complete vibrational spectrum of iron allows the identification of modes not available by other techniques. This permits the correlation of frequency with other physical properties. A significant example is the correlation we find between the Fe-Im stretch in six-coordinate Fe(XO) hemes and the trans Fe-N(Im) bond distance, not possible previously. NRVS also provides uniquely quantitative insight into the dynamics of the iron. For example, it provides a model-independent means of characterizing the strength of iron coordination. Prediction of the temperature-dependent mean-squared displacement from NRVS measurements yields a vibrational "baseline" for Fe dynamics that can be compared with results from techniques that probe longer time scales to yield quantitative insights into additional dynamical processes.

Figure 1

NRVS measurements on hemes exploit a fortuitous coincidence: Iron plays a prominent role in cellular metalloproteins, and the nuclear properties of the ⁵⁷Fe isotope are particularly favorable for NRVS. Experimental facilities have been developed at one or more synchrotron light sources to allow measurements of the nuclear resonances plotted on the left as a function of photon energy and excited state lifetime, with areas proportional to the absorption cross section. Circles filled in red (for ⁵⁷Fe) or cyan indicate resonances for which NRVS measurements have been reported. Data obtained from refs (12) and (14). Relative abundance of metalloproteins containing metals other than iron and zinc is less than 3% in P. furiosus, one of a few microorganisms for which the metalloproteome is well characterized (data reported in ref (15)).

Figure 2

Schematic diagram illustrating the experimental setup for the NRVS experiment including the high-resolution monochromator. Synchrotron beam is run in pulse mode, and avalanche photodiode, APD, is disabled during the X-ray pulse (shown bottom left) in order to gate out elastically scattered 14.4 keV photons, so that only delayed photons corresponding to nuclear absorption are detected. Lateral APD detectors measure nuclear absorption, including the vibrational signal, by detecting 6.4 and 14.4 keV fluorescence emitted by excited ⁵⁷Fe nuclei, while the coherent forward-scattered 14.4 keV photons reaching the second APD provide a real-time measure of the experimental resolution function. Photo at the left is the Advanced Photon Source at Argonne National Lab. Photo courtesy of Argonne National Laboratory.

Figure 3

ν₅₀ (top) and ν₅₃ (bottom) modes of E_u symmetry comprise the predicted vibrational dynamics of iron parallel to the porphyrin plane for the ground state of [Fe(P)]. In this and subsequent figures, each arrow is 100(m_j/m_Fe)^1/2 times longer than the zero-point vibrational amplitude of atom j. This and all subsequent illustrations of vibrational modes were rendered with the program MOLEKEL.

Figure 4

From top to bottom, respectively, γ₉, γ₆, and γ₇ modes predicted for the ground state of [Fe(P)].

Figure 5

Experimental vibrational densities of states for [Fe(P)(Cl)] and [Fe(P)(Br)].

Figure 6

Predicted vibrational character of the in-plane modes for the FeCO fragment in [Fe(TPP)(1-MeIm)(CO)] with frequencies 560 (left) and 580 cm^–1 (right) and observed at 569 and 586 cm^–1. Relative phase of the FeCO bending and porphyrin motions reverses between the 560 and 580 the cm^–1 modes. Illustration prepared using calculations originally reported in ref (67).

Figure 7

Predicted in-plane vibrational modes of [Fe(TPP)(1-MeIm) (CO)] with frequencies 318 (left) and 329 cm^–1 (right), as viewed looking from the CO to the imidazole. Note the direction of iron motion toward a porphyrin nitrogen atom. Porphyrin component of motion corresponds to γ₆. Illustration prepared using DFT calculations originally reported in ref (67).

Figure 8

Experimental and calculated NRVS vibrational density of states (VDOS) for the Fe atom in [Fe(OEP)(CO)] and [Fe(OEP)(1-MeIm)(CO)] versus wavenumber shift. Top two panels are for [Fe(OEP)(CO)], with the first panel showing the experimental NRVS measurements on an oriented single crystal. Measurements yield the directional contributions to the Fe VDOS to a polycrystalline powder. Calculated VDOS for parallel (red), perpendicular (blue), and powder (black) are shown in the second panel. Experimentally derived VDOS for powdered [Fe(OEP)(1-MeIm)(CO)] is shown in the third panel with the predicted oriented VDOS from DFT calculations, revealing the ν(Fe–C) frequency below that of δ(FeCO). Reprinted with permission from ref (79). Copyright 2014 American Chemical Society.

Figure 9

Backbonding correlation plot showing the vibrational signature of [Fe(OEP)(CO)] (solid red star), with its uniquely high experimental νFe–C frequency. Open round (green, anionic), square (magenta, neutral), and triangular (blue, trans-O-bound) points were taken from ref (82) and represent various porphyrins and proteins. Diamond (violet, trans-Tyr) points are Tyr-liganded proteins.^, Inset in the upper left shows the correlation lines based on experimental data. “5-c” line is expected for six-coordinate species with trans H₂O ligands (see ref (79)). Open star-shaped points give predicted (DFT) νFe–C and νC–O frequencies for the indicated trans ligand. Frequencies were scaled to those of [Fe(OEP)(CO)]. Reprinted with permission from ref (79). Copyright 2014 American Chemical Society.

Figure 10

Measured (lines, ref (99)) and predicted (shaded and based on an MO6L functional) contributions to the VDOS from iron motion. e_fFe² values (bars) over the 125–480 cm^–1 range are also presented. Adapted wth permission from ref (100). Copyright 2014 American Chemical Society.

Figure 11

Plots of several predicted in-plane modes for [Fe(OEP)(NO)] are shown. Directions of iron motion are either parallel and perpendicular to the FeNO plane and not along the Fe–N_p bonds. Illustration prepared using DFT results reported in ref (99).

Figure 12

Figure illustrating the predicted character of the high-frequency FeNO bending mode of monoclinic [Fe(TpFPP)(1-MeIm)(NO)] observed at 561 and 571 cm^–1 and predicted at 599 cm^–1. Note that there is less observed in-plane motion for this derivative than that of [Fe(TPP)(1-MeIm)(NO)]. Illustration prepared using calculations originally reported in ref (109).

Figure 13

Plot illustrating the predicted character of the mode most characteristic of the Fe–Im stretch in [Fe(OEP)(2-MeHIm)(NO)]⁺. Predicted frequency is 225 cm^–1, and observed frequency is 238 cm^–1. Adapted with permission from ref (110). Copyright 2014 American Chemical Society.

Figure 14

Predicted vibrational character of the Fe–O₂ unit in [Fe(TpivPP)(1-EtIm)(O₂)] for the modes observed at 571 and 417 cm^–1. Illustration prepared using DFT calculations originally reported in ref (122).

Figure 15

Change in the Fe–C–N bending (y direction) between the low- and the high-spin states of [K(222)][Fe(TPP)(CN)]. Frequencies given are predicted values. Note the substantial FeCN bending contribution to the porphyrin mode ν₅₀ at 476.7 cm^–1 that is not found in the high-spin state. Adapted with permission from ref (127). Copyright 2012 American Chemical Society.

Figure 16

Change in the in-plane (y-direction) modes between the low- and the high-spin states of [K(222)][Fe(TPP)(CN)]. Again, note the differences in porphyrin ring and iron mixing. Adapted with permission from ref (127). Copyright 2012 American Chemical Society.

Figure 17

Diagram illustrating the correlations of iron motion in the high- and low-spin states of [K(222)][Fe(TPP)(CN)]. Color coding is shown in the inset of the high-spin panel. Height of the bars gives the calculated kinetic energy contribution of iron to the mode. Horizontal axes are on the same linear scale; positions of the predicted peaks are somewhat arbitrary in order to avoid overlaps. Reprinted with permission from ref (127). Copyright 2012 American Chemical Society.

Figure 18

Comparison of the calculated kinetic energy contributions of the Fe, C, and O atoms in [Fe(OEP)(CO)] and [Fe(OEP)(1-MeIm)(CO)]. Vertical axis gives the value of the predicted kinetic energy contribution from each of the three atoms in FeCO at each frequency.

Figure 19

Plot showing the correlation of the Fe–XO stretching frequencies determined by NRVS (highest frequency chosen when two are observed) with the observed (X-ray) Fe–X bond lengths for the six-coordinate Fe(Im)(XO) derivatives. Correlation coefficient for the fit for the nonlinear Fe–X–O derivatives is 0.96.

Figure 20

Plot showing the correlation of the Fe–XO stretching frequencies determined by NRVS (highest frequency chosen when two are observed) with the observed (X-ray) Fe–X bond lengths for the five-coordinate Fe(XO) derivatives.. Correlation coefficient for the fit is 0.93.

Figure 21

Correlation between Fe–N(Im) bond distances and Fe–Im stretch frequencies (ν_Fe–Im) of six-coordinate [Fe(Porph)(RIm)(XO)] (X = N, C, O) complexes: filled triangle, [Fe(OEP)(2-MeHIm)(NO)]⁺; filled square, [Fe(TPP)(1-MeIm)(CO)]; open circles, [Fe(TpivPP)(2-MeHIm)(O2)] and [Fe(TpivPP)(1-MeIm)(O2)]; filled circle, [Fe(TPP)(1-MeIm)(NO)], tri-[Fe(TpFPP)(1-MeIm)(NO)], and mono-[Fe(TpFPP)(1-MeIm)(NO)]. Correlation coefficient for the fit is 0.94.

Figure 22

Four DFT-predicted out-of-plane Fe modes contributing to the pair of experimental features at 216 and 226 cm^–1 in [Fe(TPP)(2-MeHIm)]. Reprinted with permission from ref (134). Copyright 2012 American Chemical Society.

Figure 23

Predicted oop modes at 27, 28, and 83 cm^–1 for [Fe(TPP)(2-MeHIm)] (top); predicted mode at 87 cm^–1 is similar to the 83 cm^–1 mode. Predicted out-of-plane modes at 36 and 116 cm^–1 for [Fe(OEP)(2-MeHIm)] (bottom). Reprinted with permission from ref (134). Copyright 2012 American Chemical Society.

Figure 24

Diagram illustrating the differences in the coordination group structure and the five-membered ring geometry between the five-coordinate imidazole and imidazolate species. Number to the left in each diagram is the average F–N_p distance, middle number is the iron displacement from the four nitrogen plane, and top number is the value of the axial bond distance. Distances and angles for the ligand ring are also displayed. Reproduced from ref (137) with permission. Copyright 2015 Royal Society of Chemistry.

Figure 25

Comparison of the measured Fe VDOS in [Fe(OEP)(2-MeHIm)] in the directions parallel (top) and perpendicular (bottom) to the imidazole plane. Adapted with permission from ref (152). Copyright 2013 American Chemical Society.

Figure 26

Vibrational densities of states determined from NRVS measurements on oxidized and reduced cytochrome c. Upper panel compares the contributions expected from vibrations observed in Raman spectra, based on frequency shifts between ⁵⁴Fe- and ⁵⁷Fe-enriched samples according to eq 1. Solid black curve in the upper panel is the sum of contributions from individual Raman-active modes, indicated as dashed curves.

Figure 27

Plots of integrands in eqs 2 and 3 illustrate the relative importance of high- and low-frequency regions to determining the stiffness and resilience, respectively.

Figure 28

Comparison of effective MSDs obtained from Mössbauer measurements with the pure vibrational MSDs calculated from NRVS measurements on oxidized cyt c.

Figure 29

Comparison of the predicted MSDs obtained from the powder NRVS spectrum and the effective MSDs obtained obtained from temperature-dependent Mössbauer measurements for [Fe(TPP)(NO)].

Figure 30

Comparison of the predicted MSDs obtained from the powder NRVS spectrum and the effective MSDs obtained from a temperature-dependent Mössbauer measurement for Fe(OEP)(NO).