Multiscale Modeling of Diffusion in a Crowded Environment
- PMID: 28924915
- PMCID: PMC5747305
- DOI: 10.1007/s11538-017-0346-6
Multiscale Modeling of Diffusion in a Crowded Environment
Abstract
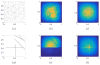
We present a multiscale approach to model diffusion in a crowded environment and its effect on the reaction rates. Diffusion in biological systems is often modeled by a discrete space jump process in order to capture the inherent noise of biological systems, which becomes important in the low copy number regime. To model diffusion in the crowded cell environment efficiently, we compute the jump rates in this mesoscopic model from local first exit times, which account for the microscopic positions of the crowding molecules, while the diffusing molecules jump on a coarser Cartesian grid. We then extract a macroscopic description from the resulting jump rates, where the excluded volume effect is modeled by a diffusion equation with space-dependent diffusion coefficient. The crowding molecules can be of arbitrary shape and size, and numerical experiments demonstrate that those factors together with the size of the diffusing molecule play a crucial role on the magnitude of the decrease in diffusive motion. When correcting the reaction rates for the altered diffusion we can show that molecular crowding either enhances or inhibits chemical reactions depending on local fluctuations of the obstacle density.
Keywords: Macromolecular crowding; Stochastic reaction–diffusion simulations.
Figures



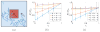
Similar articles
-
Monte Carlo simulations of enzymatic reactions in crowded media. Effect of the enzyme-obstacle relative size.Math Biosci. 2014 May;251:72-82. doi: 10.1016/j.mbs.2014.03.012. Epub 2014 Mar 26. Math Biosci. 2014. PMID: 24680707
-
Meaningful interpretation of subdiffusive measurements in living cells (crowded environment) by fluorescence fluctuation microscopy.Curr Pharm Biotechnol. 2010 Aug;11(5):527-43. doi: 10.2174/138920110791591454. Curr Pharm Biotechnol. 2010. PMID: 20553227 Free PMC article.
-
Agent-based simulation of reactions in the crowded and structured intracellular environment: Influence of mobility and location of the reactants.BMC Syst Biol. 2011 May 14;5:71. doi: 10.1186/1752-0509-5-71. BMC Syst Biol. 2011. PMID: 21569565 Free PMC article.
-
Formation of protein complexes in crowded environments--from in vitro to in vivo.FEBS Lett. 2013 Apr 17;587(8):1046-52. doi: 10.1016/j.febslet.2013.01.007. Epub 2013 Jan 18. FEBS Lett. 2013. PMID: 23337873 Free PMC article. Review.
-
Protein Aggregation and Molecular Crowding: Perspectives From Multiscale Simulations.Int Rev Cell Mol Biol. 2017;329:49-77. doi: 10.1016/bs.ircmb.2016.08.009. Epub 2016 Oct 22. Int Rev Cell Mol Biol. 2017. PMID: 28109331 Review.
Cited by
-
Excluded volume effects in on- and off-lattice reaction-diffusion models.IET Syst Biol. 2017 Apr;11(2):55-64. doi: 10.1049/iet-syb.2016.0021. IET Syst Biol. 2017. PMID: 28476973 Free PMC article.
-
Spatial Stochastic Intracellular Kinetics: A Review of Modelling Approaches.Bull Math Biol. 2019 Aug;81(8):2960-3009. doi: 10.1007/s11538-018-0443-1. Epub 2018 May 21. Bull Math Biol. 2019. PMID: 29785521 Free PMC article. Review.
-
A multiscale compartment-based model of stochastic gene regulatory networks using hitting-time analysis.J Chem Phys. 2021 May 14;154(18):184105. doi: 10.1063/5.0010764. J Chem Phys. 2021. PMID: 34241042 Free PMC article.
-
Computational Approaches to Predict Protein-Protein Interactions in Crowded Cellular Environments.Chem Rev. 2024 Apr 10;124(7):3932-3977. doi: 10.1021/acs.chemrev.3c00550. Epub 2024 Mar 27. Chem Rev. 2024. PMID: 38535831 Free PMC article. Review.
-
From membrane receptors to protein synthesis and actin cytoskeleton: Mechanisms underlying long lasting forms of synaptic plasticity.Semin Cell Dev Biol. 2019 Nov;95:120-129. doi: 10.1016/j.semcdb.2019.01.006. Epub 2019 Jan 12. Semin Cell Dev Biol. 2019. PMID: 30634048 Free PMC article. Review.
References
-
- Andrews SS, Bray D. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Phys Biol. 2004;1(3–4):137–151. - PubMed
-
- Barkai E, Garini Y, Metzler R. Strange kinetics of single molecules in living cells. Phys Today. 2012;65(8):29–35.
-
- Ben-Avraham D, Havlin S. Diffusion and reactions in fractals and disordered systems. Cambridge University Press; 2000.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

