Comparing two sequential Monte Carlo samplers for exact and approximate Bayesian inference on biological models

Abstract

Bayesian methods are advantageous for biological modelling studies due to their ability to quantify and characterize posterior variability in model parameters. When Bayesian methods cannot be applied, due either to non-determinism in the model or limitations on system observability, approximate Bayesian computation (ABC) methods can be used to similar effect, despite producing inflated estimates of the true posterior variance. Owing to generally differing application domains, there are few studies comparing Bayesian and ABC methods, and thus there is little understanding of the properties and magnitude of this uncertainty inflation. To address this problem, we present two popular strategies for ABC sampling that we have adapted to perform exact Bayesian inference, and compare them on several model problems. We find that one sampler was impractical for exact inference due to its sensitivity to a key normalizing constant, and additionally highlight sensitivities of both samplers to various algorithmic parameters and model conditions. We conclude with a study of the O'Hara-Rudy cardiac action potential model to quantify the uncertainty amplification resulting from employing ABC using a set of clinically relevant biomarkers. We hope that this work serves to guide the implementation and comparative assessment of Bayesian and ABC sampling techniques in biological models.

Keywords: approximate Bayesian computation; cardiac modelling; identifiability; sequential Monte Carlo; summary statistics.

Figure 1.

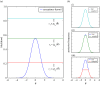
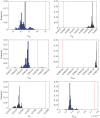
Impact of the magnitude of the normalizing constant c_ɛt of equation (2.4) on posteriors produced by a rejection sampler. The plot (a) demonstrates a sample (Gaussian) acceptance kernel function, with three potential values for the normalizing constant shown relative to an empirical estimate of the mode . Plots (b) show the true posterior (blue) along with empirical posteriors that would result from employing a sampler with an acceptance kernel normalized to a value greater than (i), slightly less than (ii) or much less than (iii) its true modal value.

Figure 2.

Schematic of the Toni SMC sampler. ‘Weighting’ encompasses lines 20–22 of algorithm 2, where importance weights are assigned to each particle to allow for sampling the next estimate. ‘Rejection sampling’ encompasses lines 7–14, where samples are drawn from the previous estimate, perturbed according to the proposal distribution, then accepted or rejected (and subsequently resampled) according to the kernel function. (Online version in colour.)

Figure 3.

Schematic of the Del Moral SMC sampler. Between rounds, particles with non-zero weights evolve according to independent Markov Chains (lines 22–25, algorithm 2) and weight calculation (lines 7–9) can happen concurrently. If the ESS falls below a critical fraction, ‘resampling’ occurs to repopulate the posterior estimate with uniformly weighted draws from the previous estimate (lines 16–21). (Online version in colour.)

Figure 4.

Visual representation of the summary statistics used by the approximate samplers for the O'Hara–Rudy action potential model. Vertical lines represent the times (ms) used for the values of APD50 and APD90 (respectively, labelled), while horizontal lines represent the voltages (mV) used for the values of peak and rest potential (respectively, labelled). The red ‘x’ indicates the point at which dV/dt (mV ms⁻¹) is greatest, i.e. the point of maximum upstroke velocity. (Online version in colour.)

Figure 5.

Posteriors generated by the (a) Toni and (b) Del Moral samplers over the linear model when using a top-hat acceptance kernel. Vertical bars represent frequencies of binned values of a among particles in the posterior estimate, while the vertical red line represents the theoretical posterior mean calculated with equation (3.2). (Online version in colour.)

Figure 6.

Effect of population size and α in the Del Moral sampler on posteriors produced over the linear model. Posteriors produced using 1000 (a) and 10 000 (b) particles at varying values of the algorithmic parameter α. Histograms parallel to the ‘a’ axis represent the frequencies of particles in the final posterior estimate generated under the corresponding value of α on the ‘alpha’ axis. Note that the a-axis has been shifted in both graphs, as noted in the bottom-left marking on each. (Online version in colour.)

Figure 7.

Posterior generated by the Del Moral sampler over the linear model when using a Gaussian acceptance kernel. (a) Histogram of particle frequencies, with the red vertical line indicating the theoretical mean. (b) Quantile–quantile plot comparing the PPF of the estimated posterior (x-axis) to that of the theoretical posterior (y-axis) by paired estimation at 100 equally spaced quantiles. (Online version in colour.)

Figure 8.

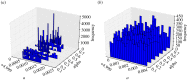
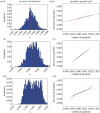
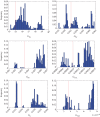
Effect of c_ɛt on posteriors generated by the Toni algorithm over the linear model with a Gaussian acceptance kernel. , where is the maximum-likelihood estimate of the slope parameter. (a) Histogram of particle frequencies, with the red vertical line indicating the theoretical mean. (b) Quantile–quantile plot comparing the PPF of the estimated posterior (x-axis) to that of the theoretical posterior (y-axis) at 100 equally spaced quantiles. (Online version in colour.)

Figure 9.

Effect of model dimension on stability of Toni and Del Moral samplers. Variance of particle weights (σ_w, plotted in log-scale) in the approximate Toni sampler (a) and both the approximate (b) and exact (c) Del Moral samplers, each with 1000 particles, as they iterate over posterior estimates of the polynomial model with increasing numbers of parameters (indicated by their ‘order’). Iteration of the algorithm is marked on the x-axis (log-scale) by the value of the algorithmic threshold parameter (ɛ_t).

Figure 10.

Selected marginal distributions from the posterior produced by the exact Del Moral algorithm on the 13-parameter O'Hara–Rudy model. Inference was performed using full time trace data. Generating values for the simulated data are indicated by vertical red lines. (Online version in colour.)

Figure 11.

Selected marginal distributions from the posterior produced by the approximate Del Moral algorithm on the 13-parameter O'Hara–Rudy model. Inference was performed using summary statistic data. Generating values for the simulated data are indicated by vertical red lines. (Online version in colour.)