Biological and statistical processes jointly drive population aggregation: using host-parasite interactions to understand Taylor's power law
- PMID: 28931738
- PMCID: PMC5627205
- DOI: 10.1098/rspb.2017.1388
Biological and statistical processes jointly drive population aggregation: using host-parasite interactions to understand Taylor's power law
Abstract
The macroecological pattern known as Taylor's power law (TPL) represents the pervasive tendency of the variance in population density to increase as a power function of the mean. Despite empirical illustrations in systems ranging from viruses to vertebrates, the biological significance of this relationship continues to be debated. Here we combined collection of a unique dataset involving 11 987 amphibian hosts and 332 684 trematode parasites with experimental measurements of core epidemiological outcomes to explicitly test the contributions of hypothesized biological processes in driving aggregation. After using feasible set theory to account for mechanisms acting indirectly on aggregation and statistical constraints inherent to the data, we detected strongly consistent influences of host and parasite species identity over 7 years of sampling. Incorporation of field-based measurements of host body size, its variance and spatial heterogeneity in host density accounted for host identity effects, while experimental quantification of infection competence (and especially virulence from the 20 most common host-parasite combinations) revealed the role of species-by-environment interactions. By uniting constraint-based theory, controlled experiments and community-based field surveys, we illustrate the joint influences of biological and statistical processes on parasite aggregation and emphasize their importance for understanding population regulation and ecological stability across a range of systems, both infectious and free-living.
Keywords: community ecology; disease ecology; feasible sets; macroecology; population regulation; superspreaders.
© 2017 The Author(s).
Conflict of interest statement
We have no competing interests.
Figures
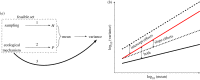

 , p < 0.001; slope
, p < 0.001; slope , p = 0.072). (d) Same as (c) but points are coloured according to parasite species. Parasite species identity affects both the intercept and slope of the residual variation (intercept
, p = 0.072). (d) Same as (c) but points are coloured according to parasite species. Parasite species identity affects both the intercept and slope of the residual variation (intercept  , p < 0.01; slope
, p < 0.01; slope , p < 0.01).
, p < 0.01).

Similar articles
-
When can we infer mechanism from parasite aggregation? A constraint-based approach to disease ecology.Ecology. 2017 Mar;98(3):688-702. doi: 10.1002/ecy.1675. Epub 2017 Feb 3. Ecology. 2017. PMID: 27935638
-
Heterogeneous hosts: how variation in host size, behaviour and immunity affects parasite aggregation.J Anim Ecol. 2014 Sep;83(5):1103-12. doi: 10.1111/1365-2656.12215. Epub 2014 Mar 17. J Anim Ecol. 2014. PMID: 24548254
-
Why apply ecological laws to epidemiology?Trends Parasitol. 2008 Jul;24(7):304-9. doi: 10.1016/j.pt.2008.04.003. Trends Parasitol. 2008. PMID: 18514576
-
Review of the trematode genus Ribeiroia (Psilostomidae): ecology, life history and pathogenesis with special emphasis on the amphibian malformation problem.Adv Parasitol. 2004;57:191-253. doi: 10.1016/S0065-308X(04)57003-3. Adv Parasitol. 2004. PMID: 15504539 Review.
-
Host-multiparasite interactions in amphibians: a review.Parasit Vectors. 2021 Jun 3;14(1):296. doi: 10.1186/s13071-021-04796-1. Parasit Vectors. 2021. PMID: 34082796 Free PMC article. Review.
Cited by
-
On Spatiotemporal Overdispersion and Macroparasite Accumulation in Hosts Leading to Aggregation: A Quantitative Framework.Diseases. 2022 Dec 27;11(1):4. doi: 10.3390/diseases11010004. Diseases. 2022. PMID: 36648869 Free PMC article.
-
The Distribution and Host-Association of the Vector Chigger Species Leptotrombidium imphalum in Southwest China.Insects. 2024 Jul 5;15(7):504. doi: 10.3390/insects15070504. Insects. 2024. PMID: 39057237 Free PMC article.
-
Identifying sources of variation in parasite aggregation.PeerJ. 2022 Aug 24;10:e13763. doi: 10.7717/peerj.13763. eCollection 2022. PeerJ. 2022. PMID: 36039371 Free PMC article.
-
Spatial and temporal autocorrelations affect Taylor's law for US county populations: Descriptive and predictive models.PLoS One. 2021 Jan 7;16(1):e0245062. doi: 10.1371/journal.pone.0245062. eCollection 2021. PLoS One. 2021. PMID: 33412569 Free PMC article.
-
Chance or choice? Understanding parasite selection and infection in multi-host communities.Int J Parasitol. 2019 Apr;49(5):407-415. doi: 10.1016/j.ijpara.2018.12.007. Epub 2019 Mar 17. Int J Parasitol. 2019. PMID: 30894285 Free PMC article.
References
-
- Taylor LR. 1961. Aggregation, variance and the mean. Nature 169, 732–735. (10.1038/189732a0) - DOI
-
- Anderson RM, Gordon DM, Crawley MJ, Hassell MP. 1982. Variability in the abundance of animal and plant species. Nature 296, 245–248. (10.1038/296245a0) - DOI
-
- Downing JA. 1986. Spatial heterogeneity: evolved behaviour or mathematical artefact? Nature 323, 255–257. (10.1038/323255a0) - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

