Decoherence Control of Nitrogen-Vacancy Centers
- PMID: 28931932
- PMCID: PMC5607330
- DOI: 10.1038/s41598-017-12280-z
Decoherence Control of Nitrogen-Vacancy Centers
Abstract
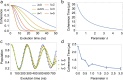
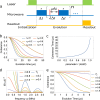
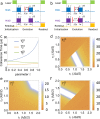
Quantum mechanical systems lose coherence through interacting with external environments-a process known as decoherence. Although decoherence is detrimental for most of the tasks in quantum information processing, a substantial degree of decoherence is crucial for boosting the efficiency of quantum processes, for example, in quantum biology and other open systems. The key to the success in simulating those open quantum systems is therefore the ability of controlling decoherence, instead of eliminating it. Motivated by simulating quantum open systems with Nitrogen-Vacancy centers, which has become an increasingly important platform for quantum information processing tasks, we developed a new set of steering pulse sequences for controlling various coherence times of Nitrogen-Vacancy centers; our method is based on a hybrid approach that exploits ingredients in both digital and analog quantum simulations to dynamically couple or decouple the system with the physical environment. Our numerical simulations, based on experimentally-feasible parameters, indicate that decoherence of Nitrogen-Vacancy centers can be controlled externally to a very large extend.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures
Similar articles
-
Quantum decoherence and quasi-equilibrium in open quantum systems with few degrees of freedom: application to 1H NMR of nematic liquid crystals.J Chem Phys. 2011 Dec 28;135(24):244509. doi: 10.1063/1.3668559. J Chem Phys. 2011. PMID: 22225171
-
Solid-state electronic spin coherence time approaching one second.Nat Commun. 2013;4:1743. doi: 10.1038/ncomms2771. Nat Commun. 2013. PMID: 23612284
-
Cavity QED implementation of non-adiabatic holonomies for universal quantum gates in decoherence-free subspaces with nitrogen-vacancy centers.Opt Express. 2015 Jun 1;23(11):14027-35. doi: 10.1364/OE.23.014027. Opt Express. 2015. PMID: 26072772
-
Deconvolving Contributions to Decoherence in Molecular Electron Spin Qubits: A Dynamic Ligand Field Approach.Chemistry. 2021 Jul 2;27(37):9482-9494. doi: 10.1002/chem.202100845. Epub 2021 May 17. Chemistry. 2021. PMID: 33855760 Review.
-
Spin-Mechanics with Nitrogen-Vacancy Centers and Trapped Particles.Micromachines (Basel). 2021 Jun 1;12(6):651. doi: 10.3390/mi12060651. Micromachines (Basel). 2021. PMID: 34206001 Free PMC article. Review.
Cited by
-
Nitrogen-Vacancy Color Centers Created by Proton Implantation in a Diamond.Materials (Basel). 2021 Feb 9;14(4):833. doi: 10.3390/ma14040833. Materials (Basel). 2021. PMID: 33572415 Free PMC article.
-
Optical tomography dynamics induced by qubit-resonator interaction under intrinsic decoherence.Sci Rep. 2022 Oct 13;12(1):17162. doi: 10.1038/s41598-022-21348-4. Sci Rep. 2022. PMID: 36229509 Free PMC article.
References
-
- Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21 (1982).
-
- Lloyd, S. Universal quantum simulators. Science273 (1996). - PubMed
-
- Yung, M.-H., Whitfield, J. D., Boixo, S., Tempel, D. G. & Aspuru-Guzik, A. Introduction to Quantum Algorithms for Physics and Chemistry. In Kais, S. (ed.) Adv. Chem. Phys., vol. 154, 67–106 (John Wiley & Sons, Inc., New Jersey, 2014).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

