Phase changes in neuronal postsynaptic spiking due to short term plasticity

Abstract

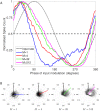
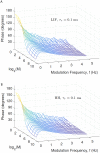
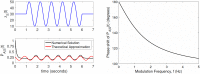
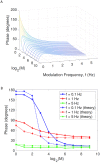
In the brain, the postsynaptic response of a neuron to time-varying inputs is determined by the interaction of presynaptic spike times with the short-term dynamics of each synapse. For a neuron driven by stochastic synapses, synaptic depression results in a quite different postsynaptic response to a large population input depending on how correlated in time the spikes across individual synapses are. Here we show using both simulations and mathematical analysis that not only the rate but the phase of the postsynaptic response to a rhythmic population input varies as a function of synaptic dynamics and synaptic configuration. Resultant phase leads may compensate for transmission delays and be predictive of rhythmic changes. This could be particularly important for sensory processing and motor rhythm generation in the nervous system.

Fig 1. Conceptual diagram of the overall model and examples of different synaptic configurations.

As shown in Subfigure A, we assume a total of M independent pre-synaptic neurons each make multiple synaptic contacts with a post-synaptic neuron. We refer to each pre-synaptic neuron as forming a single active-zone, and assume each active zone has N_M sites that each probabilistically release a single-vesicle when activated by a pre-synaptic action-potential, if one is available at that site. The post-synaptic neuron is assumed to be depolarized by arrival of neurotransmitter resulting from release of vesicles, according to standard models of AMPA receptors. Subfigure B shows a total of N = 512 vesicle release sites are equally distributed between M active zones. Each active zone is the target of a single presynaptic axon (arrows) being driven by a unique input neuron. We refer to the case of a single active zone (M = 1) as the “giant” synaptic pathway, and the case of 512 active zones (M = 512) as the “cortical” synaptic pathway.

Fig 2. Raster plots and time-dependent histograms of simulated postsynaptic spiking of the model, in response to f = 1 Hz modulated pre-synaptic population inputs for different synaptic configurations with depressing synapses.

The first panel shows the pre-synaptic spike-rate modulation, λ_S(t). The second panel shows the spike times of 10 independently generated pre-synaptic spike trains with time-dependent inhomogenous Poisson rate λ_S(t). The third, fifth and seventh panels show 10 post-synaptic spike responses for three distinct synaptic configurations (M = 1, M = 4 and M = 32), in response to 10 sets of independent pre-synaptic spike-trains. The fourth, sixth and eighth panels show histograms of the number of post-synaptic spikes as a function of time, in 5 ms bins, from 100 independent input spike-trains, and 100 independent trials for the vesicle releases for each input spike-train.

Fig 3. The phase of output spiking depends on synaptic configuration.

The traces in Subfigure A were produced by forming histograms of postsynaptic spiking in response to 1 Hz-modulated population inputs for different synaptic configurations with depressing synapses. Spike times from each cycle of the input modulation in all cells in all runs with a particular synaptic configuration were binned in 1.8° phase bins. The histograms were then smoothed using a 20 sample moving average, and normalised. The dotted line shows the phase of the input modulation; since the modulation is defined as a sine wave rather than a cosine wave, the phase of its peak is at 90°, whereas the output spiking peaks at an earlier phase, and therefore has a phase lead. The dashed line makes it clear that the largest output phase lead (the blue trace crosses the dashed line at approximately 90° to the left of where the input modulation crosses the dashed line) is for M = 1 and the smallest (approximately 40°) for M = 512. Subfigure B shows scatter plots of each pair of phase and normalised spike count used to form the data shown in subfigure A; colored lines indicate the mean phase, in good correspondence with the crossings of the dashed line shown in A. The dotted black line shows that the phase of the input modulation is 90°, as in subfigure A.

Fig 4. Phase lead of output spiking responses, relative to the periodic modulation of Poisson pre-synaptic spiking.

Data is for both the LIF and Hodgkin-Huxley models, each with a rise time of 0.1 ms. As shown in S1 Fig, the phase change as a function of modulation frequency and the number of pre-synaptic neurons, M, is very similar when the post-synaptic conductance change has no rise-time.

Fig 5. Theoretical calculations of phase shift.

The lower left panel shows that for a modulation frequency of f = 1 Hz, our mathematical derivation of an approximate steady state solution to Eq (10) correctly obtains the phase shift in the conditional vesicle availability probability, P_A|S(t), relative to periodic input spike rate modulation, λ_S(t). In the legend, ‘Theoretical’ corresponds to Eq (12). Parameter values are as shown in Table 3. The right-side panel is shown to make it clear that there is a large phase shift relative to the input stimulation. The phase shift according to a numerical integration of Eq (21) is 144.54° for the numerical solution and 146.52° for the theoretical solutions. The right panel shows the theoretically calculated phase shift (Eq (13)) of conditional vesicle availability probability, P_A|S(t). The phase shift is relative to periodic input spike rate modulation, λ_S(t), as a function of modulation frequency, f.

Fig 6. Theoretical approximation of Eq (18).

Subfigure A, obtained with τ_p = 30 ms, shows that our theoretical prediction of the phase shift is strongly in qualitative agreement in terms of the trend with M and f obtained from simulations and shown in Fig 4. Subfigure B shows that the quantitative agreement is superior for larger values of M and f; here we have adjusted τ_p independently for each value of f, namely τ_p = 10 ms for f = 0.1 Hz, τ_p = 30 ms for f = 1 Hz, and τ_p = 60 ms for f = 5 Hz.

Fig 7. Theoretical analysis of resonance in phase change vs system dynamics.

Subfigures A and C show, for M = 512, that the mathematically predicted resonance in the phase change observed in Fig 6A depends strongly on the longest time constant in the system, τ_rec and on the vesicle release probability, P_v. Subfigures B and D show, for M = 512, that the period of the resonance has an approximately linear relationship with $\sqrt{{\tau }_{\text{rec}}}$ and $\sqrt{P_{\mathrm{v}}}$. Together, τ_rec and P_v determine the time course of depression, which determines phase.