Melanoma screening: Informing public health policy with quantitative modelling

Abstract

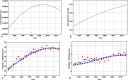
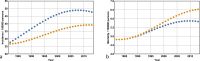
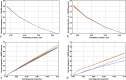
Australia and New Zealand share the highest incidence rates of melanoma worldwide. Despite the substantial increase in public and physician awareness of melanoma in Australia over the last 30 years-as a result of the introduction of publicly funded mass media campaigns that began in the early 1980s -mortality has steadily increased during this period. This increased mortality has led investigators to question the relative merits of primary versus secondary prevention; that is, sensible sun exposure practices versus early detection. Increased melanoma vigilance on the part of the public and among physicians has resulted in large increases in public health expenditure, primarily from screening costs and increased rates of office surgery. Has this attempt at secondary prevention been effective? Unfortunately epidemiologic studies addressing the causal relationship between the level of secondary prevention and mortality are prohibitively difficult to implement-it is currently unknown whether increased melanoma surveillance reduces mortality, and if so, whether such an approach is cost-effective. Here I address the issue of secondary prevention of melanoma with respect to incidence and mortality (and cost per life saved) by developing a Markov model of melanoma epidemiology based on Australian incidence and mortality data. The advantages of developing a methodology that can determine constraint-based surveillance outcomes are twofold: first, it can address the issue of effectiveness; and second, it can quantify the trade-off between cost and utilisation of medical resources on one hand, and reduced morbidity and lives saved on the other. With respect to melanoma, implementing the model facilitates the quantitative determination of the relative effectiveness and trade-offs associated with different levels of secondary and tertiary prevention, both retrospectively and prospectively. For example, I show that the surveillance enhancement that began in 1982 has resulted in greater diagnostic incidence and reduced mortality, but the reduced mortality carried a significant cost per life saved. I implement the model out to 2028 and demonstrate that the enhanced secondary prevention that began in 1982 becomes increasingly cost-effective over the period 2013-2028. On the other hand, I show that reductions in mortality achieved by significantly enhancing secondary prevention beyond 2013 levels are comparable with those achieved by only modest improvements in late-stage disease survival. Given the ballooning costs of increased melanoma surveillance, I suggest the process of public health policy decision-making-particularly with respect to the public funding of melanoma screening and discretionary mole removal-would be better served by incorporating the results of quantitative modelling.

Fig 1

(a) State transitions represented by a directed graph. (b) The associated transition matrix. In both (a) and (b) undiagnosed (U) and diagnosed (D) disease are shown in yellow and light blue respectively. An iteration of the model corresponds to 1 year. Note the rows sum to 1 since the probability of transitioning to the same state is given by 1 minus the sum of all other entries for that row. The diagonal entry for Stage 1 in yellow thus represents the finite probability that an individual can remain with undiagnosed disease for many years, in keeping with the observation that some patients will not present in a timely manner [28], or their doctor may not make an early diagnosis [29]. This phenomenon increases the likelihood that he or she may transition directly to undiagnosed later-stage disease.

Fig 2. Monte-Carlo sensitivity analysis.

(a) Deviations in melanoma incidence. (b), Deviations in melanoma mortality. (c) Deviations in the prevalence of diagnosed thin melanoma. All deviations are calculated with respect to the model parameters. For a given parameter, the model was run to steady state for each of 10,000 normally distributed random values about its 1982 steady state value (with a standard deviation of 10% of the steady state value) while keeping all other parameters fixed at the values that yield the 1982 steady state (where zero deviation is given by an incidence of 27.08 per year per 100,000 persons, a mortality of 4.76 per year per 100,000 persons and the prevalence of diagnosed thin melanoma of 3215 per 100,000 persons). Note how the majority of variability within the model is due to variation in the time-dependent variables I(t) and D(t), with the exception of the value of q which has a disproportionate influence on mortality.

Fig 3. The Markov model for D(0) = 0.05 and p = 15.

(a) The true incidence curve I(t) = 0.00031 + 0.00068t – 0.00056t² (t is rescaled) for the period 1982–2013. Note how this curve peaks around 2003. (b) The detection likelihood, D(t) = 0.05 + 0.075t – 0.075t² (t is rescaled) corresponding to the probability of diagnosis of Stage 1 melanoma per year in an individual with hitherto undetected Stage 1 melanoma. Note the incremental increase over the period 1982–2013. (c) Actual incidence data (orange dots), least-squares curve of best fit to these data (continuous line), and the Markov approximation (blue dots) over the period 1982–2013. Note the accuracy of the Markov approximation, and note how this curve peaks later than the true incidence curve given by (a). (d) Mortality data with the same interpretation as (c). Note the increase in mortality from ~5 persons per year per 100,000 persons in 1982 to ~6 persons per year per 100,000 persons in 2013. (All actual incidence and mortality data are reported at the Australian Institute of Health and Welfare website [15]).

Fig 4. The effects of enhanced secondary prevention for the years 1982–2013.

(a) Diagnostic incidence curves. (b) Mortality curves. For both plots, enhanced secondary prevention is represented by the blue dots while secondary prevention that remains at 1982 levels is represented by the orange dots. Note how a lack of enhanced secondary prevention results in a lower diagnostic incidence rate but an increased and divergent mortality rate.

Fig 5. The effects of improved efficacy associated with treating late-stage disease and the effects of over-diagnosis for the years 1982–2013.

(a) Average mortality reductions per year per 100,000 persons as a function of q for all p where D(0) = 0.01 and (b) D(0) = 0.05. Note the robustness of results with respect to both p and D(t) (all five plots for different values of p are closely superimposed). (c) Excess diagnoses per 100,000 persons as a function of maximal over-diagnosis proportion for all p where D(0) = 0.01 and (d) D(0) = 0.05.

Fig 6. Expected melanoma incidence and mortality for the years 2013–2028.

(a) Extending enhanced secondary prevention at its 2013 level to 2028 (where incidence is given by the orange dots) compared with a continuation of 1982 levels (blue dots) reveals a converging diagnostic incidence rate and (b) a divergent mortality rate. (c) Reverting to the 1982 detection probabilities of Stage I melanoma in 2013 results in a sharp drop in diagnostic incidence that rebounds rapidly, and (d) a divergent mortality curve. (e) Reducing the risk of death from late-stage disease in any year by half in 2013 results in no change to incidence and (f) a sharp drop in mortality that quickly rebounds to baseline levels.

Fig 7. The expected effects associated with improved efficacy in treating late-stage disease for the years 2013–2028.

(a) D(0) = 0.01. (b) D(0) = 0.05. Projected reductions in mortality (per year per 100,000 persons) as a consequence of increased likelihood of surviving the effects of late-stage disease for all values of p. Note the robustness of results for all 10 models (all the lines representing different values of p are nearly superimposed).