A theory that predicts behaviors of disordered cytoskeletal networks
- PMID: 28954810
- PMCID: PMC5615920
- DOI: 10.15252/msb.20177796
A theory that predicts behaviors of disordered cytoskeletal networks
Abstract
Morphogenesis in animal tissues is largely driven by actomyosin networks, through tensions generated by an active contractile process. Although the network components and their properties are known, and networks can be reconstituted in vitro, the requirements for contractility are still poorly understood. Here, we describe a theory that predicts whether an isotropic network will contract, expand, or conserve its dimensions. This analytical theory correctly predicts the behavior of simulated networks, consisting of filaments with varying combinations of connectors, and reveals conditions under which networks of rigid filaments are either contractile or expansile. Our results suggest that pulsatility is an intrinsic behavior of contractile networks if the filaments are not stable but turn over. The theory offers a unifying framework to think about mechanisms of contractions or expansion. It provides the foundation for studying a broad range of processes involving cytoskeletal networks and a basis for designing synthetic networks.
Keywords: actin; active gel; cell cortex; contractility; morphogenesis.
© 2017 The Authors. Published under the terms of the CC BY 4.0 license.
Figures
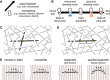
- A
Networks are composed of polar filaments that may bend, and connectors containing two subunits through which they can bridge two nearby filaments.
- B
Subunits may be minus‐end‐ or plus‐end‐directed motors that can bind anywhere to a filament, or binders that can bind to any location along a filament, or end binders that attach only at the minus or the plus ends of filaments.
- C, D
To predict the behavior of a network, previous theories have considered a pair of filaments with a single connector between them, while the theory presented here is based on the effects that two connectors bound to a single filament have on the rest of the network.
- E
Pairs of connectors may generate local stress in the network depending on how the subunits move relative to one another on the filament. If the initial distance a 0 between the subunits is maintained, the network does not deform. This occurs if the connectors do not move (in static configurations) or if they move in the same direction at the same speed (in neutral configuration). Local contraction is expected for contractile configuration in which the connectors move toward each other (a < a 0) and expansion may occur for extensile configuration where the connectors move apart (a > a 0). If the filament is flexible, however, the expansile stress can be reduced if the filament buckles.

A system composed of flexible filaments and two types of connectors: crosslinkers and bifunctional motors. The table lists the four possible configurations for two connectors bound to a filament, the relative movement of the connectors (), and the likelihood and the mechanical nature of each configuration. The likelihoods are combinations of P M and P C, which are the probabilities of having at least one motor or one crosslinker at an intersection of two filaments (see Appendix Supplementary Methods D).
The evolution of a simulated random network composed of 1,500 flexible filaments (bending rigidity = 0.01 pN μm2) and 12,000 connectors of each type, distributed over a circular area of radius 15 μm.
The contraction rate of a simulated network as a function of the ratio of crosslinkers to motors, with the total number of connectors kept constant. Each symbol indicates the result of one simulation. The broken line indicates the analytical prediction made by the theory (see Appendix Supplementary Methods D). No contraction occurs without crosslinkers or without motors, and the maximal contractile rate is obtained here for 8,000 motors and 10,000 crosslinkers.
Snapshots at t = 10 s of networks similar to (B) containing varying numbers of motors (vertical axis) and crosslinkers (horizontal axis).

A system composed of rigid filaments and two types of connectors. One connector consists of a plus‐end‐directed motor combined with a minus‐end binder, the other is a plus‐end‐directed motor combined with a plus‐end binder. There are six possible configurations involving these two connectors.
Three time points during the evolution of an expansile network of 1,500 straight filaments (their bending rigidity is set as “infinite” here) with 1,500 motor/plus‐end binders and 48,000 motor/minus‐end binders initially distributed over a circular area of radius 15 μm.
Three time points during the evolution of a network similar as (B), but with 48,000 motor/plus‐end binders and 1,500 motor/minus‐end binders.
The contraction rate of a network as a function of the numbers of the two types of connectors, which are inversely varied. Each symbol represents a simulated random network of 4,000 straight filaments initially distributed over a circular area of radius 25 μm. Details of methods as in Fig 2C. The broken line indicates the analytical prediction made by the theory (Appendix Supplementary Methods G).
Simulations of networks containing varying numbers of connectors. Networks contain 1,500 filaments initially distributed over a radius of 15 μm. Depending on the concentrations of the connectors, the network can be expansile (top left corner) or contractile (bottom right corner). Snapshots at t = 30 s.

Examples of simulations of networks with the indicated types of connectors. The predicted outcomes of network contraction, expansion, or neutrality (symbol at the top left of each simulation) are confirmed in each case by the behavior of the network in simulations. The networks are composed of 1,500 flexible or rigid filaments, and 24,000 connectors. Snapshots at t = 20 s.
Summary of the predictions for random networks with all possible combinations with two types of connectors, either with flexible (bending rigidity = 0.01 pN μm2, below diagonal) or rigid filaments (infinite rigidity, above diagonal). The networks contain 4,000 filaments and 64,000 connectors, 32,000 of each connector type, indicated by the labels of the corresponding row and column. These results were generated using Preconfig (Nedelec, 2017).
Comparison of the contraction rates predicted by the theory (horizontal axis) with the rates obtained by simulation (vertical axis). Each data point indicates one of the 210 systems considered in (B). Networks are made of 4,000 filaments and 64,000 connectors initially distributed over a circular area of radius 25 μm. In this case, all the binding parameters of the subunits and the concentration of connectors are always equal, such that the prediction is simplified (Appendix Supplementary Methods E).

- A
Configurations present in a heterogeneous network containing rigid minifilaments and flexible actin‐like filaments. The motors are permanently attached at the extremities of the minifilaments, so as to represent myosin minifilaments. The system is predicted to be contractile in the presence of passive crosslinkers connecting actin filaments directly, and neutral without crosslinkers.
- B
Detail of a simulation with minifilaments (green) and crosslinkers (blue).
- C, D
The simulated systems contract only if crosslinkers are included.
- E
Time series of a simulation with filament turnover, 1,400 filaments (rigidity 0.075 pN μm2), 22,400 motors, 5,600 crosslinkers within periodic boundary conditions with size 16 μm. Filament turnover was implemented by deleting a randomly selected filament and placing a new filament at a random location, stochastically with a rate R = 64 s−1, corresponding to an average filament lifetime of ˜21.8 s. The series shows the formation of a new contractile spot (black arrowhead) and its downward movement and fusion with another contractile spot (green arrowheads).
- F
The local density of filaments in an arbitrarily chosen region covering ˜6% of the simulated space as a function of time. The data with filament lifetime 21.8 s are from the simulation shown in (A). The network continues to redistribute, showing irregular variations of the local filament density, and does not collapse into one spot.
References
-
- Backouche F, Haviv L, Groswasser D, Bernheim‐Groswasser A (2006) Active gels: dynamics of patterning and self‐organization. Phys Biol 3: 264–273 - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

