Quantitative Deformability Cytometry: Rapid, Calibrated Measurements of Cell Mechanical Properties

Abstract

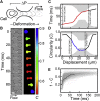
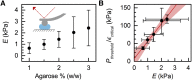
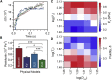
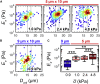
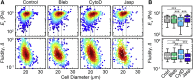
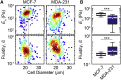
Advances in methods that determine cell mechanical phenotype, or mechanotype, have demonstrated the utility of biophysical markers in clinical and research applications ranging from cancer diagnosis to stem cell enrichment. Here, we introduce quantitative deformability cytometry (q-DC), a method for rapid, calibrated, single-cell mechanotyping. We track changes in cell shape as cells deform into microfluidic constrictions, and we calibrate the mechanical stresses using gel beads. We observe that time-dependent strain follows power-law rheology, enabling single-cell measurements of apparent elastic modulus, E_a, and power-law exponent, β. To validate our method, we mechanotype human promyelocytic leukemia (HL-60) cells and thereby confirm q-DC measurements of E_a = 0.53 ± 0.04 kPa. We also demonstrate that q-DC is sensitive to pharmacological perturbations of the cytoskeleton as well as differences in the mechanotype of human breast cancer cell lines (E_a = 2.1 ± 0.1 and 0.80 ± 0.19 kPa for MCF-7 and MDA-MB-231 cells). To establish an operational framework for q-DC, we investigate the effects of applied stress and cell/pore-size ratio on mechanotype measurements. We show that E_a increases with applied stress, which is consistent with stress stiffening behavior of cells. We also find that E_a increases for larger cell/pore-size ratios, even when the same applied stress is maintained; these results indicate strain stiffening and/or dependence of mechanotype on deformation depth. Taken together, the calibrated measurements enabled by q-DC should advance applications of cell mechanotype in basic research and clinical settings.

Figure 1

Cell-shape changes during transit through microfluidic constrictions. (A) Schematic of a single cell transiting through a micron-scale constriction by pressure-driven flow, where ΔP is the pressure drop across the cell. Cell shape is evaluated by measuring circularity, C(t) = 4πA(t)/P(t)², during transit, and the time-dependent strain, ϵ(t), is defined as 1 − C(t). (B) Time sequence of a representative HL-60 cell transiting through a microfluidic constriction that exhibits the median transit time and cell size of the cell population. The white border illustrates the cell boundary, as detected by our imaging algorithm. The color overlay illustrates the change in circularity, C, during deformation. Scale bar, 15 μm. (C and D) Timescale and shape change during transit through a microfluidic constriction. The x axis represents the position of the centroid of the cell. We extract (C) transit time, which is the time required for the leading edge of the cell to enter and exit the constriction region, and (D) time-dependent strain or creep, which is determined by the changes in shape (circularity) of the cell as it deforms into the pore. The creep time begins when the leading edge of the cell enters the constriction and ends when the centroid exits the constriction, as illustrated by the dashed lines. (E) Creep trajectories for the population of HL-60 cells (N = 550). The gray dotted lines represent data from individual cells. The solid gray line represents the creep trajectory of the representative HL-60 cell.

Figure 2

Stress calibration using agarose gel particles. (A) Elastic moduli of gel particles made with varying concentrations of agarose from 1.0 to 3.0 % (w/w) as measured by AFM. Data represent the average ± SD for N = 12–53 particles over two independent experiments. (B) Agarose calibration particles are used to determine the applied stresses in the q-DC device by measuring the minimum threshold pressure, P_threshold, required to induce a critical strain, ϵ_critical, for a particle to deform through a constricted channel. Shown here are representative data for N > 140 particles transiting through a 5 × 5 μm channel. Horizontal error bars represent the standard deviation of the elastic modulus, as indicated by the vertical error bars in (A). Vertical error bars represent the standard deviation of the threshold-pressure/particle-strain ratio. The line is the linear fit determined by the Deming method. The shaded region illustrates the 95% confidence interval of the fit. The inverse of the slope characterizes the calibration factor, A. To see this figure in color, go online.

Figure 3

PLR for cell mechanotyping by q-DC. (A) Creep trajectory for a single, representative HL-60 cell (gray dots). Lines represent the least-squares fits of viscoelastic models to the creep data: Maxwell (red dotted line), Kelvin-Voigt (KV, purple long-dashed line), SLS (blue dot-dashed line), and PLR (green short-dashed line). (B) Residuals for the least-squares fits of the viscoelastic models to the creep trajectories of a population of HL-60 cells (N = 550), as shown in Fig. 1E. Shown here are the bootstrapped median residuals; error bars represent the bootstrapped confidence interval. ^∗p < 0.05, ^∗∗∗p$\ll$ 0.001. (C and D) Heat maps show (C) the apparent elastic modulus, E_a, and (D) the fluidity, β, of HL-60 cells as a function of transit time, T_T, and cell diameter, D_cell, which is measured in the microfluidic channel before the cell enters the constriction. Each bin represents the median E_a or β of N = 3–47 single cells.

Figure 4

Mechanotype of HL-60 cells depends on applied pressure and cell/pore-size ratio. (A) Density scatter plots show apparent elastic modulus, E_a, as a function of cell size. The cell diameter, D_cell, is measured in the microfluidic channel before the cell enters the constriction. Data represent the deformation response for HL-60 cells that are driven to deform through 5 × 10 μm constrictions with increasing applied pressure. The calibrated applied stress is shown on the bottom right corner of each plot. Dots represent single-cell data. Cell size, measured by q-DC, increases with applied pressure, as there is a higher probability that larger cells will transit at higher pressures; at lower pressures, larger cells have a higher probability of occluding constrictions. To compare data sets, we bin cells by the median cell diameter, as indicated by the gray dashed lines; the resultant size-binned data are shown in the boxplots in (C). (B) Density scatter plot illustrating the elastic modulus, E_a, as a function of cell size for HL-60 cells deforming through 9 × 10 μm constrictions. (C) Boxplots show the size-gated distributions of E_a for HL-60 cells with D_cell = 16 ± 1 μm. Cells are subject to varying applied stresses, $\overline{\sigma }$, and constriction geometries: white lines represent the median, boxes represent the interquartile ranges, whiskers represent the 10th and 90th percentiles, and white squares represent the bootstrapped median. N > 200 for each cell type. Statistical significance is determined using the Mann-Whitney U test: ^∗∗p < 0.01, ^∗∗∗p < 0.001. To see this figure in color, go online.

Figure 5

Mechanotyping of HL-60 cells treated with cytoskeleton-perturbing drugs using q-DC. HL-60 cells are treated with blebbistatin (Bleb), cytochalasin D (CytoD), and jasplakinolide (Jasp). (A) Density scatter plots show apparent elastic modulus, E_a, and fluidity, β, as functions of cell size, which is measured in the microfluidic channel before the cell enters the constriction. The cell diameter shown here appears to be larger than unconfined cells (Fig. S8A), as well as cells in the 10 μm height devices (Fig. 4), due to axial compression that occurs when the cell diameter is larger than the device height. Each dot represents a single cell. To compare data sets, we bin cells by size, as depicted by the dotted lines. Cell-size distributions are shown in Fig. S8. (B) Boxplots represent the size-binned distributions of E_a and β for cells with D_cell = 21 ± 1 μm, white lines represent the median, boxes represent the interquartile ranges, whiskers represent the 10th and 90th percentiles, and white squares represent the bootstrapped median. N > 500 for each cell type. Statistical significance is determined using the Mann-Whitney U test: ^∗∗p < 0.01, ^∗∗∗p < 0.001. To see this figure in color, go online.

Figure 6

Mechanotyping of human breast cancer cell lines using q-DC. (A) Density scatter plots show E_a and β as functions of cell size for MCF-7 and MDA-231 cell lines. To compare cell populations, we bin data by cell size, as depicted by the dotted lines. Cell diameter is measured in the microfluidic channel before the cell enters the constriction. (B) Boxplots represent the size-binned distributions of E_a and β for cells with D_cell = 21 ± 1 μm. White lines represent the median. Boxes denote the interquartile ranges and whiskers denote the 10th–90th percentiles. White squares represent the bootstrapped medians. N > 100 for each cell type. The Mann-Whitney U test is used to determine statistical significance: ^∗∗p < 0.01, ^∗∗∗p < 0.001. To see this figure in color, go online.