Forecasting seasonal influenza with a state-space SIR model

Abstract

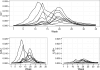
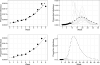
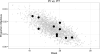
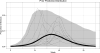
Seasonal influenza is a serious public health and societal problem due to its consequences resulting from absenteeism, hospitalizations, and deaths. The overall burden of influenza is captured by the Centers for Disease Control and Prevention's influenza-like illness network, which provides invaluable information about the current incidence. This information is used to provide decision support regarding prevention and response efforts. Despite the relatively rich surveillance data and the recurrent nature of seasonal influenza, forecasting the timing and intensity of seasonal influenza in the U.S. remains challenging because the form of the disease transmission process is uncertain, the disease dynamics are only partially observed, and the public health observations are noisy. Fitting a probabilistic state-space model motivated by a deterministic mathematical model [a susceptible-infectious-recovered (SIR) model] is a promising approach for forecasting seasonal influenza while simultaneously accounting for multiple sources of uncertainty. A significant finding of this work is the importance of thoughtfully specifying the prior, as results critically depend on its specification. Our conditionally specified prior allows us to exploit known relationships between latent SIR initial conditions and parameters and functions of surveillance data. We demonstrate advantages of our approach relative to alternatives via a forecasting comparison using several forecast accuracy metrics.

Keywords: Bayesian modeling; SIR model; forecasting; influenza; state-space modeling; time-series.

Fig. 1

ILI+ (top), ILIA+, and ILIB+ (bottom) for influenza seasons 2002–2007 and 2010–2013. Weeks 1 and 35 roughly correspond to the beginning of October and the end of May, respectively.

Fig. 2

Simulated SIR curve with S₀ = 0.9, I₀ = 0.0002, R₀ = 0.0998, β = 2, and γ = 1.4.

Fig. 3

The mean process defined by equation (4.1b) for two sets of parameters are displayed. The parameters corresponding to the dashed trajectory (top) are ${\theta }_0^S=0.9$, ${\theta }_0^I=0.000172$, ${\theta }_0^R=0.099828$, β = 2.22, γ = 1.7017, and κ = 20,000. The parameters corresponding to the dotted trajectory (bottom) are ${\theta }_0^S=0.9$, ${\theta }_0^I=0.00018$, ${\theta }_0^R=0.09982$, β = 0.3912, γ = 0.077, and κ = 20,000. Points are 2010 ILI+ observations for weeks one through nine. Grey lines are the ILI+ trajectories for years 2002–2007 and 2011–2013 for weeks 10 through 35.

Fig. 4

The peak intensity (PI) on the y-axis vs. the timing of peak intensity (PT) on the x-axis for years 2002–2007 and 2010–2013 (black points). 10,000 samples were drawn from the truncated normal distribution of equation (6.10) with ${\theta }_0^I=0.0002$ and plotted in grey.

Fig. 5

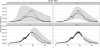
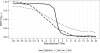
The median (thick black line) and 95% prediction intervals (grey band) based on M = 5000 draws from the prior predictive distribution. Historical ILI+ observations are displayed for reference (thin grey lines).

Fig. 6

95% posterior predictive intervals for [y_(t′+1):T|y_1:t′] (light grey bands) and 95% credible intervals for $[{\theta }_0^I,{\theta }_1^I,\cdots ,{\theta }_{t\prime }^I|y_{1:t\prime }]$ (dark grey bands). Posterior medians (black lines) and ILI+ observations (points) are also displayed for the 2010 nationwide, influenza seasons. The number at the top of each panel is t′. All plots are based on 5000 simulations.

Fig. 7

Distribution of M1, M2, and M3 scores for the DBSSM (top) and SM2 (bottom).

Fig. 8

P̂(PT > t′|y_1:t′) averaged over all scenarios versus standardized time.