Liver segmentation from CT images using a sparse priori statistical shape model (SP-SSM)
- PMID: 28981530
- PMCID: PMC5628825
- DOI: 10.1371/journal.pone.0185249
Liver segmentation from CT images using a sparse priori statistical shape model (SP-SSM)
Abstract
This study proposes a new liver segmentation method based on a sparse a priori statistical shape model (SP-SSM). First, mark points are selected in the liver a priori model and the original image. Then, the a priori shape and its mark points are used to obtain a dictionary for the liver boundary information. Second, the sparse coefficient is calculated based on the correspondence between mark points in the original image and those in the a priori model, and then the sparse statistical model is established by combining the sparse coefficients and the dictionary. Finally, the intensity energy and boundary energy models are built based on the intensity information and the specific boundary information of the original image. Then, the sparse matching constraint model is established based on the sparse coding theory. These models jointly drive the iterative deformation of the sparse statistical model to approximate and accurately extract the liver boundaries. This method can solve the problems of deformation model initialization and a priori method accuracy using the sparse dictionary. The SP-SSM can achieve a mean overlap error of 4.8% and a mean volume difference of 1.8%, whereas the average symmetric surface distance and the root mean square symmetric surface distance can reach 0.8 mm and 1.4 mm, respectively.
Conflict of interest statement
Figures
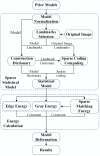











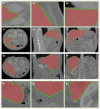
References
-
- Salman AlShaikhli SD, Yang MY, Rosenhahn B. Brain tumor classification and segmentation using sparse coding and dictionary learning. Biomedical Engineering-biomedizinische Technik. 2016;61(4):413 doi: 10.1515/bmt-2015-0071 - DOI - PubMed
-
- Kato T, Hino H, Murata N. Multi-frame image super resolution based on sparse coding. Neural Networks the Official Journal of the International Neural Network Society. 2015;66(C):64 doi: 10.1016/j.neunet.2015.02.009 - DOI - PubMed
-
- Afzali M, Ghaffari A, Fatemizadeh E, Soltanian-Zadeh H. Medical image registration using sparse coding of image patches. Computers in Biology & Medicine. 2016;73(C):56–70. - PubMed
-
- Khormuji MK, Bazrafkan M. A novel sparse coding algorithm for classification of tumors based on gene expression data. Medical & Biological Engineering & Computing. 2016;54(6):869. - PubMed
-
- Ptucha R, Savakis AE. LGE-KSVD: robust sparse representation classification. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society. 2014;23(4):1737–50. doi: 10.1109/TIP.2014.2303648 - DOI - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

