Chemotherapeutic Dose Scheduling Based on Tumor Growth Rates Provides a Case for Low-Dose Metronomic High-Entropy Therapies
- PMID: 28986381
- PMCID: PMC5712269
- DOI: 10.1158/0008-5472.CAN-17-1120
Chemotherapeutic Dose Scheduling Based on Tumor Growth Rates Provides a Case for Low-Dose Metronomic High-Entropy Therapies
Abstract
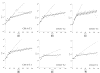
We extended the classical tumor regression models such as Skipper's laws and the Norton-Simon hypothesis from instantaneous regression rates to the cumulative effect over repeated cycles of chemotherapy. To achieve this end, we used a stochastic Moran process model of tumor cell kinetics coupled with a prisoner's dilemma game-theoretic cell-cell interaction model to design chemotherapeutic strategies tailored to different tumor growth characteristics. Using the Shannon entropy as a novel tool to quantify the success of dosing strategies, we contrasted MTD strategies as compared with low-dose, high-density metronomic strategies (LDM) for tumors with different growth rates. Our results show that LDM strategies outperformed MTD strategies in total tumor cell reduction. This advantage was magnified for fast-growing tumors that thrive on long periods of unhindered growth without chemotherapy drugs present and was not evident after a single cycle of chemotherapy but grew after each subsequent cycle of repeated chemotherapy. The evolutionary growth/regression model introduced in this article agrees well with murine models. Overall, this model supports the concept of designing different chemotherapeutic schedules for tumors with different growth rates and develops quantitative tools to optimize these schedules for maintaining low-volume tumors. Cancer Res; 77(23); 6717-28. ©2017 AACR.
©2017 American Association for Cancer Research.
Conflict of interest statement
The authors declare no potential conflicts of interest.
Figures

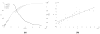
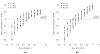



References
-
- Nowak M. Stochastic strategies in the prisoner’s dilemma. Theoretical Population Biology. 1990;38:93–112.
-
- Lien K, Georgsdottir S, Sivanathan L, Chan K, Emmenegger U. Low-dose metronomic chemotherapy: a systematic literature analysis. European Journal of Cancer. 2013;49:3387–3395. - PubMed
-
- Kerbel RS, Kamen BA. The anti-angiogenic basis of metronomic chemotherapy. Nature Reviews Cancer. 2004;4:423–436. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

