Relating cell shape and mechanical stress in a spatially disordered epithelium using a vertex-based model

Abstract

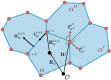
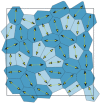
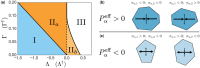
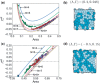
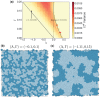
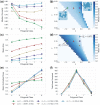
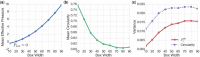
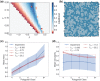
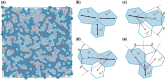
Using a popular vertex-based model to describe a spatially disordered planar epithelial monolayer, we examine the relationship between cell shape and mechanical stress at the cell and tissue level. Deriving expressions for stress tensors starting from an energetic formulation of the model, we show that the principal axes of stress for an individual cell align with the principal axes of shape, and we determine the bulk effective tissue pressure when the monolayer is isotropic at the tissue level. Using simulations for a monolayer that is not under peripheral stress, we fit parameters of the model to experimental data for Xenopus embryonic tissue. The model predicts that mechanical interactions can generate mesoscopic patterns within the monolayer that exhibit long-range correlations in cell shape. The model also suggests that the orientation of mechanical and geometric cues for processes such as cell division are likely to be strongly correlated in real epithelia. Some limitations of the model in capturing geometric features of Xenopus epithelial cells are highlighted.

Fig. 1.

Experimental setup and data analysis. (a) Animal cap tissue was dissected from stage-10 Xenopus laevis embryos and cultured on PDMS membrane. (b) Side-view confocal image of the animal cap (top:apical; bottom:basal), stained for microtubules (red), beta-catenin (green) and DNA (blue). A mitotic spindle is visible in the centremost apical cell. The animal cap is a multi-layered epithelial tissue; we analyse just the outer, apical, cell layer. (c) The apical cell layer of the animal cap tissue is imaged live using confocal microscopy (green, GFP--tubulin; red, cherry-histone2B). (d) The cell edges are manually traced and cell shapes are derived computationally, being polygonized using the positions of cell junctions. (e) Mean normalized area as a function of polygonal class showing mean and one standard deviation, from experiments (solid and shaded) and simulation (dashed) with parameters , as shown with . Cell areas were normalized relative to the mean of each experiment. (f) Circularity as a function of polygonal class showing mean and one standard deviation, from experiments (solid and shaded) and simulation (dashed) using the same parameters as in (e). (g) Proportions of total cells in each polygonal class in experiments (left bar) and simulations (right bar). Error bars represent confidence intervals calculated from bootstrapping the data. (Colour in online.)

Fig. 2.

Representation of disordered cell geometry. Cell has its centroid at relative to a fixed origin, . The position of vertex of cell is given equivalently via , relative to the centroid, or , relative to . For a vertex (trijunction) at , there exist three vectors, for cells, , pointing to the same vertex. Cell properties, such as area and tangents along edges, are defined relative to the cell centroid. (Colour in online.)

Fig. 3.

Computational validation of the predicted alignment between principal axis of stress and shape, for . The initial cell array was generated using a Voronoi tessellation and then relaxed to equilibrium using periodic boundary conditions. The eigenvectors corresponding the the principal eigenvalue of and are plotted in black and yellow, respectively. Darker cells have (net tension); lighter cells have (net compression). (Colour in online.)

Fig. 4.

(a) -parameter space, showing boundaries for a uniform hexagonal array (following Farhadifar et al., 2007). Region I represents a ‘soft’ network with no shear resistance, bounded by (3.38); has a single positive root in region II and two positive roots in region . The network collapses in Region III, which is bounded by and (3.39). The transformation (3.40) allows to be replaced by in order to describe cases for which . (b,c) Classification of cell stress configurations in a disordered monolayer, showing representative cell shapes. Larger (smaller) arrows indicate the orientation of the eigenvector associated with the eigenvalue of the stress tensor having larger (smaller) magnitude, where . Inward- (outward)-pointing arrows indicate the tension (compression) generated by the cell. (Colour in online.)

Fig. 5.

(a, c) Curves show defined in (3.37) plotted against cell area for perfect N-gons, using (, a, b) and (, c, d). Symbols show defined in (3.24) for computationally simulated cells, with shapes displayed in (b,d). Darker (lighter) cells in (b,d) have (). (Colour in online.)

Fig. 6.

(a) A map of the variance of at discrete locations within region II of -parameter space. Lines show the boundaries for a hexagonal network, as in Fig. 4(a). The dark squares along the region II/III boundary are artefacts, reflecting the co-existence of cells with small and large areas near this boundary. Each datapoint is taken from 5 realizations of a monolayer with 800 cells. (b) An individual monolayer realization for , , with 800 cells. Darker (lighter) shading denotes cells with . Line segments indicate the principal axis of the shape and stress tensor for each cell, coincident with the heavy arrows in Fig. 4(b), i.e. aligned with the stress eigenvector associated with the eigenvalue of larger magnitude. (c) A similar example for , . (Colour in online.)

Fig. 7.

Dependence of cell geometry on model parameters, using five unique simulations with 800 cells (4000 cells total) in a periodic box under zero net external pressure. (a) Mean circularity of cells per polygonal class, at parameter values indicated by corresponding symbols in -parameter space in (b,c). (b) The heat map shows mean circularity of all cells in a simulation, using the same realizations used in Fig. 6. Insets show two example configurations. (c) Mean cell area per polygonal classes, for the same set of parameters. (d) Heat map of mean area of all cells across -parameter space. (e) Mean cell area per polygonal class for given parameters, normalised by the mean area of hexagons. (f) Total area of all cells in each polygonal class, such that the sum of all points equals the area of the box. (Colour in online.)

Fig. 8.

Visualizing the effect of peripheral stress on network packing geometry. 800 cells were simulated in boxes of width leading to distributions with means shown in (a). for a box width of 20. The corresponding means of the distributions of circularities are shown in (b). The variance of the distributions at different box widths are given in (c), for (solid) and circularity (dashed). Model parameters used were for which . Larger box sizes have lower cell density, higher mean , lower mean circularity and greater variability. (Colour in online.)

Fig. 9.

Results of parameter fitting. (a) Heat map showing value of the likelihood function (4.1) across a uniform grid in valid parameter space. The simulated monolayers used were the same as those in Figs 6 and 7. For each monolayer, the mean areas per polygonal class were calculated and used to evaluate (4.1). The likelihood was maximized at , marked by the circular symbol; a corresponding monolayer is shown in (b), with cells having () shaded dark (light). (c, d) Distributions of area and circularity across polygonal classes for simulations with for increasing values of . (Colour in online.)

Fig. D1.

(a) An example of force chains in a monolayer, with 800 cells and , , . Darker (lighter) shading denotes cells with . Short line segments indicate the principal axis of the stress tensor for each cell (see Fig. 4). Long red lines identify chains satisfying (D.1) with . (b–e) identify force chains. Red lines represent vectors running between cell centroids. Black double sided arrows indicate the principal axis of stress. b) Cell has been selected to start a chain, and cells and are found to satisfy (D.1c). (c-e) Only is selected to join the chain as it satisfies both (D.1a) (c) and (D.1b) (d). is excluded because is fails (D.1a) (c), despite satisfying (D.1b) (e). (Colour in online.)