Fragmentation transitions in a coevolving nonlinear voter model
- PMID: 28993664
- PMCID: PMC5634441
- DOI: 10.1038/s41598-017-13047-2
Fragmentation transitions in a coevolving nonlinear voter model
Abstract
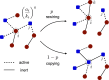
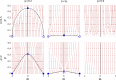
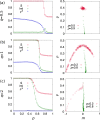
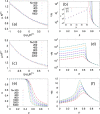
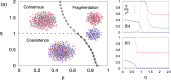
We study a coevolving nonlinear voter model describing the coupled evolution of the states of the nodes and the network topology. Nonlinearity of the interaction is measured by a parameter q. The network topology changes by rewiring links at a rate p. By analytical and numerical analysis we obtain a phase diagram in p,q parameter space with three different phases: Dynamically active coexistence phase in a single component network, absorbing consensus phase in a single component network, and absorbing phase in a fragmented network. For finite systems the active phase has a lifetime that grows exponentially with system size, at variance with the similar phase for the linear voter model that has a lifetime proportional to system size. We find three transition lines that meet at the point of the fragmentation transition of the linear voter model. A first transition line corresponds to a continuous absorbing transition between the active and fragmented phases. The other two transition lines are discontinuous transitions fundamentally different from the transition of the linear voter model. One is a fragmentation transition between the consensus and fragmented phases, and the other is an absorbing transition in a single component network between the active and consensus phases.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures
Similar articles
-
Spontaneous symmetry breaking of active phase in coevolving nonlinear voter model.Phys Rev E. 2020 Oct;102(4-1):042313. doi: 10.1103/PhysRevE.102.042313. Phys Rev E. 2020. PMID: 33212744
-
Noise in coevolving networks.Phys Rev E Stat Nonlin Soft Matter Phys. 2015 Sep;92(3):032803. doi: 10.1103/PhysRevE.92.032803. Epub 2015 Sep 8. Phys Rev E Stat Nonlin Soft Matter Phys. 2015. PMID: 26465524
-
Fitting in and breaking up: A nonlinear version of coevolving voter models.Phys Rev E. 2020 Jun;101(6-1):062303. doi: 10.1103/PhysRevE.101.062303. Phys Rev E. 2020. PMID: 32688568
-
Emergence of complex structures from nonlinear interactions and noise in coevolving networks.Sci Rep. 2020 Sep 24;10(1):15660. doi: 10.1038/s41598-020-72662-8. Sci Rep. 2020. PMID: 32973287 Free PMC article.
-
Nonlinear q-voter model.Phys Rev E Stat Nonlin Soft Matter Phys. 2009 Oct;80(4 Pt 1):041129. doi: 10.1103/PhysRevE.80.041129. Epub 2009 Oct 26. Phys Rev E Stat Nonlin Soft Matter Phys. 2009. PMID: 19905295
Cited by
-
Coevolutionary Dynamics with Global Fields.Entropy (Basel). 2022 Sep 3;24(9):1239. doi: 10.3390/e24091239. Entropy (Basel). 2022. PMID: 36141125 Free PMC article.
-
Structural transition in social networks: The role of homophily.Sci Rep. 2019 Mar 13;9(1):4310. doi: 10.1038/s41598-019-40990-z. Sci Rep. 2019. PMID: 30867537 Free PMC article.
-
Competing contagion processes: Complex contagion triggered by simple contagion.Sci Rep. 2018 Jul 10;8(1):10422. doi: 10.1038/s41598-018-28615-3. Sci Rep. 2018. PMID: 29991815 Free PMC article.
-
Deep Learning Exploration of Agent-Based Social Network Model Parameters.Front Big Data. 2021 Sep 29;4:739081. doi: 10.3389/fdata.2021.739081. eCollection 2021. Front Big Data. 2021. PMID: 34661097 Free PMC article.
-
Threshold Cascade Dynamics in Coevolving Networks.Entropy (Basel). 2023 Jun 13;25(6):929. doi: 10.3390/e25060929. Entropy (Basel). 2023. PMID: 37372273 Free PMC article.
References
-
- Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang DU. Complex networks: Structure and dynamics. Physics Reports. 2006;424:175–308. doi: 10.1016/j.physrep.2005.10.009. - DOI
-
- Barrat, A., Barthelemy, M. & Vespignani, A. Dynamical processes on complex networks. (Cambridge university press, 2008).
-
- Barabási A-L, Albert R. Emergence of scaling in random networks. Science. 1999;286:5439. - PubMed
-
- McPherson JM, Smith-Lovin L, Cook J. Birds of a feather: Homophily in social networks. Ann. Rev. Sociol. 2001;27:415–444. doi: 10.1146/annurev.soc.27.1.415. - DOI
-
- Centola D, González-Avella JC, Eguíluz VM, San Miguel M. Homophily, cultural drift, and the co-evolution of cultural groups. J. of Conflict Resol. 2007;51:905. doi: 10.1177/0022002707307632. - DOI
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

