Stress Introduction Rate Alters the Benefit of AcrAB-TolC Efflux Pumps

Abstract

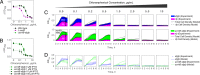
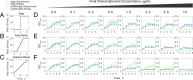
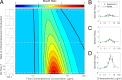
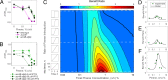
Stress tolerance studies are typically conducted in an all-or-none fashion. However, in realistic settings-such as in clinical or metabolic engineering applications-cells may encounter stresses at different rates. Therefore, how cells tolerate stress may depend on its rate of appearance. To address this, we studied how the rate of stress introduction affects bacterial stress tolerance by focusing on a key stress response mechanism. Efflux pumps, such as AcrAB-TolC of Escherichia coli, are membrane transporters well known for the ability to export a wide variety of substrates, including antibiotics, signaling molecules, and biofuels. Although efflux pumps improve stress tolerance, pump overexpression can result in a substantial fitness cost to the cells. We hypothesized that the ideal pump expression level would involve a rate-dependent trade-off between the benefit of pumps and the cost of their expression. To test this, we evaluated the benefit of the AcrAB-TolC pump under different rates of stress introduction, including a step, a fast ramp, and a gradual ramp. Using two chemically diverse stresses, the antibiotic chloramphenicol and the jet biofuel precursor pinene, we assessed the benefit provided by the pumps. A mathematical model describing these effects predicted the benefit as a function of the rate of stress introduction. Our findings demonstrate that as the rate of introduction is lowered, stress response mechanisms provide a disproportionate benefit to pump-containing strains, allowing cells to survive beyond the original inhibitory concentrations.IMPORTANCE Efflux pumps are ubiquitous in nature and provide stress tolerance in the cells of species ranging from bacteria to mammals. Understanding how pumps provide tolerance has far-reaching implications for diverse fields, from medicine to biotechnology. Here, we investigated how the rate of stressor appearance impacts tolerance. We focused on two distinct substrates of AcrAB-TolC efflux pumps, the antibiotic chloramphenicol and the biofuel precursor pinene. Interestingly, tolerance is highly dependent on the rate of stress introduction. Therefore, it is important to consider not only the total quantity of a stressor but also the rate at which it is applied. The implications of this work are significant because environments are rarely static; antibiotic concentrations change during dosing, and metabolic engineering processes change with time.

Keywords: antibiotics; biofuels; dynamic environment; efflux pumps; stress tolerance.

FIG 1

Benefits and costs of AcrAB-TolC efflux pumps. (A) Cell density as a function of chloramphenicol concentration. The wild type is E. coli BW25113, the knockout strain is E. coli BW25113 ΔacrB, and the acrAB-sfgfp strain is E. coli BW25113 ΔacrB transformed with plasmid pBbA5k-acrAB-sfgfp, which contains an IPTG-inducible promoter controlling a transcriptional fusion of the acrAB efflux pump operon and the gene for sfGFP (sfgfp). ΔOD₇₀₀ is the difference between the OD₇₀₀ of the initial sample at t = 0 h and that at t = 24 h. (B) Induction of acrAB-sfgfp reduces cell growth. The error bars in panels A and B show the standard deviations of three biological replicates. (C) Growth of two competing strains exposed to different chloramphenicol doses. The full dose of chloramphenicol was added at the beginning of the experiment (t = 0 h). The plots depict the total cell density of the coculture, and the stacked shaded areas under the curve quantify the fraction of the culture containing either an rfp or an sfgfp plasmid (Fig. S1). As a control, the top row shows competition between two strains lacking efflux pumps (sfgfp and rfp strains). The bottom row shows competition between a strain with the efflux pump (acrAB-sfgfp strain) and one without the efflux pump (rfp strain). Dots show experimental data with error bars corresponding to standard deviations of three biological replicates. Lines are the computational model predictions for the total population and the rfp strain. (D) Data extracted from the multispecies competition experiments shown in panel C comparing strains with and without pumps. The biomass of the acrAB-sfgfp strain is compared with the biomass of the sfgfp strain. Data points show mean values and standard deviations from three biological replicates; solid lines show mathematical model predictions.

FIG 2

The rate of chloramphenicol addition affects survival. (A to C) Three different rates of chloramphenicol introduction, a step (A), a fast ramp (B), and a gradual ramp (C), are shown. The thick solid line shows the values used in the mathematical model; the thin solid line shows the experimental treatment used to approximate the constant introduction rate. The total amounts of chloramphenicol added in panels A to C are equal. (D to F) Competitive growth under different rates of chloramphenicol addition. The growth of the acrAB-sfgfp strain is compared to the growth of the sfgfp strain in the competition experiments (dots), and model predictions (solid lines) for different chloramphenicol introduction rates as shown in panels A to C, respectively, are shown. As in Fig. 1D, these data were extracted from competition experiment data. Note that dead cells can still cloud the solution; therefore, nonzero ODs do not necessarily imply that cells are alive. Data points show mean values and standard deviations of three biological replicates.

FIG 3

Model predictions and experiments measuring the benefit of pumps. (A) Contour plot of the benefit ratio of efflux pumps. Model predictions for biomass, N, of an acrB-containing strain in relation to that of a ΔacrB mutant control strain after 8 h are used to predict the benefit ratio landscape. The plot shows results for different maximum levels of chloramphenicol and different rates of chloramphenicol addition. (B to D) Experimental results showing the benefit of efflux pumps compared to model predictions. Data are ratios of the biomasses of the acrAB-sfgfp and sfgfp strains after 8 h. The rates of antibiotic introduction are shown in Fig. 2A to C, respectively, and denoted by the white dashed lines on the contour plot in panel A. Error bars show the standard deviations of three biological replicates.

FIG 4

Benefit and cost trade-offs of AcrAB-TolC efflux pumps in pinene. (A) Cell density as a function of the pinene concentration. The wild type is E. coli BW25113, the knockout strain is E. coli BW25113 ΔacrB, and the rescue strain is the acrAB-sfgfp strain. ΔOD₇₀₀ is the difference between the OD₇₀₀ of the initial sample at t = 0 h and that at t = 8 h. (B) Induction of acrAB-sfgfp reduces cell growth in the presence of pinene. Error bars in panels A and B show the standard error of three biological replicates. (C) Contour plot of the benefit ratio of the efflux pumps. Model predictions for biomass of an acrB-containing strain in relation to a ΔacrB mutant strain after 8 h. The plot shows results for different maximum levels of pinene and different rates of pinene addition. (D to F) Experimental results showing the benefit of efflux pumps compared to model predictions. Data are ratios of biomasses of the acrAB-sfgfp and sfgfp strains after 8 h. The rates of pinene introduction are shown in Fig. S6A to C, respectively, and denoted by the dashed lines on the contour plot in panel C. Error bars show the standard deviations of three biological replicates.