Machine learning accelerates MD-based binding pose prediction between ligands and proteins

Abstract

Motivation: Fast and accurate prediction of protein-ligand binding structures is indispensable for structure-based drug design and accurate estimation of binding free energy of drug candidate molecules in drug discovery. Recently, accurate pose prediction methods based on short Molecular Dynamics (MD) simulations, such as MM-PBSA and MM-GBSA, among generated docking poses have been used. Since molecular structures obtained from MD simulation depend on the initial condition, taking the average over different initial conditions leads to better accuracy. Prediction accuracy of protein-ligand binding poses can be improved with multiple runs at different initial velocity.

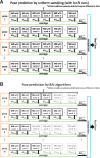
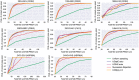
Results: This paper shows that a machine learning method, called Best Arm Identification, can optimally control the number of MD runs for each binding pose. It allows us to identify a correct binding pose with a minimum number of total runs. Our experiment using three proteins and eight inhibitors showed that the computational cost can be reduced substantially without sacrificing accuracy. This method can be applied for controlling all kinds of molecular simulations to obtain best results under restricted computational resources.

Availability and implementation: Code and data are available on GitHub at https://github.com/tsudalab/bpbi.

Contact: terayama@cbms.k.u-tokyo.ac.jp or tsuda@k.u-tokyo.ac.jp.

Supplementary information: Supplementary data are available at Bioinformatics online.

Fig. 1.

Pose prediction using uniform sampling (A) and BAI (B) algorithms. The purpose of pose prediction is to select the best (minimum $\overline{\Delta G_{20\text{vel}.}}$) pose among N prepared docking poses. Using uniform sampling, the same number (k) of MD and MM-PBSA runs with different initial velocities is performed, resulting in a total of k × N runs. On the other hand, the total number of runs can be reduced by optimally controlling runs using a BAI algorithm (B) (Color version of this figure is available at Bioinformatics online.)

Fig. 2.

The basic idea for our framework. (A) A flowchart of the BAI algorithm in the general setting. The purpose is to find the best arm (slot) by repeating selection and reward acquisition within a limited budget. (B) The BAI algorithm applied to the binding pose prediction problem. We can reduce the total number of MD and MM-PBSA runs to find the binding pose by efficient BAI algorithms (Color version of this figure is available at Bioinformatics online.)

Fig. 3.

Problem formulation of BAI

Fig. 4.

The distributions of calculated $\Delta G_{\text{bind}}s$ for all poses in eight compounds. Twenty $\Delta G_{\text{bind}}$ values are calculated for each pose. Red poses are the correct binding poses (RMSD < 2.0 Å) and blue ones are incorrect. Horizontal lines represent within boxes the mean values and indicate the mean value and the first and last quartile, while the ends of the whiskers show maximum and minimum values within 1.5 IQR (inter-quartile range: the distance between the first and last quartiles) of the first and last quartiles (Color version of this figure is available at Bioinformatics online.)

Fig. 5.

Reductions of MD and MM-PBSA runs per pose by BAI algorithms in a pose prediction trial. Green bars show the numbers of runs (k = 10) per pose by uniform sampling in a pose prediction trial. Blue, purple, red and orange bars show the number of runs per pose using UGapE auto, UCB-E auto, SR and UCB(p) (p = 4). Black lines are the averaged binding free energies ($\overline{\Delta G_{20\text{vel}.}}$). The total numbers of runs by BAI algorithms are reduced from 200 (10 × 20 poses) by uniform sampling to 50 and 75 without reducing the number of runs for promising poses, which have small $\overline{\Delta G_{20\text{vel}.}}$ values (Color version of this figure is available at Bioinformatics online.)

Fig. 6.

The probabilities of correct pose prediction by the proposed methods and uniform sampling (baseline) at different numbers of MD and MM-PBSA runs for eight complexes. The total numbers of MD and MM-PBSA runs (computational cost) were reduced using the BAI algorithms [UGapE auto, UCB-E auto, UCB(p) p = 4 and SR] without sacrificing accuracy compared to uniform sampling (green). The probabilities of UGapE auto (blue) and UCB-E auto (purple), whose exploration parameters were automatically adjusted, are higher than those of uniform sampling (green). Although UCB(p) showed almost the same high performance as UGapE auto and UCB-E auto under the exploration parameter p = 4, the result varies depending on the parameter as shown in Supplementary Figure S3. The result using SR (red) is a little worse than other BAI algorithms (Color version of this figure is available at Bioinformatics online.)