Distinguishing Among Modes of Convergent Adaptation Using Population Genomic Data
- PMID: 29046403
- PMCID: PMC5714468
- DOI: 10.1534/genetics.117.300417
Distinguishing Among Modes of Convergent Adaptation Using Population Genomic Data
Abstract
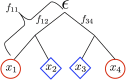
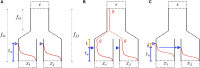
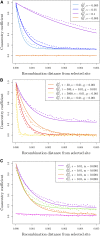
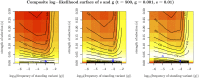
Geographically separated populations can convergently adapt to the same selection pressure. Convergent evolution at the level of a gene may arise via three distinct modes. The selected alleles can (1) have multiple independent mutational origins, (2) be shared due to shared ancestral standing variation, or (3) spread throughout subpopulations via gene flow. We present a model-based, statistical approach that utilizes genomic data to detect cases of convergent adaptation at the genetic level, identify the loci involved and distinguish among these modes. To understand the impact of convergent positive selection on neutral diversity at linked loci, we make use of the fact that hitchhiking can be modeled as an increase in the variance in neutral allele frequencies around a selected site within a population. We build on coalescent theory to show how shared hitchhiking events between subpopulations act to increase covariance in allele frequencies between subpopulations at loci near the selected site, and extend this theory under different models of migration and selection on the same standing variation. We incorporate this hitchhiking effect into a multivariate normal model of allele frequencies that also accounts for population structure. Based on this theory, we present a composite-likelihood-based approach that utilizes genomic data to identify loci involved in convergence, and distinguishes among alternate modes of convergent adaptation. We illustrate our method on genome-wide polymorphism data from two distinct cases of convergent adaptation. First, we investigate the adaptation for copper toxicity tolerance in two populations of the common yellow monkey flower, Mimulus guttatus We show that selection has occurred on an allele that has been standing in these populations prior to the onset of copper mining in this region. Lastly, we apply our method to data from four populations of the killifish, Fundulus heteroclitus, that show very rapid convergent adaptation for tolerance to industrial pollutants. Here, we identify a single locus at which both independent mutation events and selection on an allele shared via gene flow, either slightly before or during selection, play a role in adaptation across the species' range.
Keywords: coalescent theory; composite likelihood; convergent adaptation; genetic hitchhiking; positive selection.
Copyright © 2017 by the Genetics Society of America.
Figures

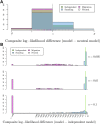


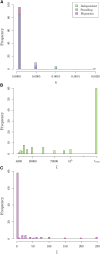
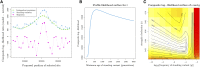
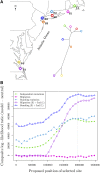
Similar articles
-
Population genomics of rapid evolution in natural populations: polygenic selection in response to power station thermal effluents.BMC Evol Biol. 2019 Feb 26;19(1):61. doi: 10.1186/s12862-019-1392-5. BMC Evol Biol. 2019. PMID: 30808292 Free PMC article.
-
A Coalescent Model for a Sweep of a Unique Standing Variant.Genetics. 2015 Oct;201(2):707-25. doi: 10.1534/genetics.115.178962. Epub 2015 Aug 25. Genetics. 2015. PMID: 26311475 Free PMC article.
-
Signatures of selection in natural populations adapted to chronic pollution.BMC Evol Biol. 2008 Oct 10;8:282. doi: 10.1186/1471-2148-8-282. BMC Evol Biol. 2008. PMID: 18847479 Free PMC article.
-
Divergence hitchhiking and the spread of genomic isolation during ecological speciation-with-gene-flow.Philos Trans R Soc Lond B Biol Sci. 2012 Feb 5;367(1587):451-60. doi: 10.1098/rstb.2011.0260. Philos Trans R Soc Lond B Biol Sci. 2012. PMID: 22201174 Free PMC article. Review.
-
Identifying adaptive alleles in the human genome: from selection mapping to functional validation.Hum Genet. 2021 Feb;140(2):241-276. doi: 10.1007/s00439-020-02206-7. Epub 2020 Jul 29. Hum Genet. 2021. PMID: 32728809 Review.
Cited by
-
Molecular Parallelism Underlies Convergent Highland Adaptation of Maize Landraces.Mol Biol Evol. 2021 Aug 23;38(9):3567-3580. doi: 10.1093/molbev/msab119. Mol Biol Evol. 2021. PMID: 33905497 Free PMC article.
-
Repeated evolution of herbicide resistance in Lolium multiflorum revealed by haplotype-resolved analysis of acetyl-CoA carboxylase.Evol Appl. 2023 Nov 20;16(12):1969-1981. doi: 10.1111/eva.13615. eCollection 2023 Dec. Evol Appl. 2023. PMID: 38143902 Free PMC article.
-
Rapid Parallel Adaptation to Anthropogenic Heavy Metal Pollution.Mol Biol Evol. 2021 Aug 23;38(9):3724-3736. doi: 10.1093/molbev/msab141. Mol Biol Evol. 2021. PMID: 33950261 Free PMC article.
-
Tensor Decomposition-based Feature Extraction and Classification to Detect Natural Selection from Genomic Data.Mol Biol Evol. 2023 Oct 4;40(10):msad216. doi: 10.1093/molbev/msad216. Mol Biol Evol. 2023. PMID: 37772983 Free PMC article.
-
Repeated Selection of Alternatively Adapted Haplotypes Creates Sweeping Genomic Remodeling in Stickleback.Genetics. 2018 Jul;209(3):921-939. doi: 10.1534/genetics.117.300610. Epub 2018 May 24. Genetics. 2018. PMID: 29794240 Free PMC article.
References
-
- Arendt J., Reznick D., 2008. Convergence and parallelism reconsidered: what have we learned about the genetics of adaptation? Trends Ecol. Evol. 23: 26–32. - PubMed
-
- Aubury L. E., 1902. The Copper Resources of California (No. 23). Superintendent State Printing, Sacramento, CA.
-
- Barrett R. D., Schluter D., 2008. Adaptation from standing genetic variation. Trends Ecol. Evol. 23: 38–44. - PubMed
-
- Barton N., 1998. The effect of hitch-hiking on neutral genealogies. Genet. Res. 72: 123–133.
-
- Barton N., Bengtsson B. O., 1986. The barrier to genetic exchange between hybridising populations. Heredity 57: 357–376. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

