MESOSCOPIC MODELING OF STOCHASTIC REACTION-DIFFUSION KINETICS IN THE SUBDIFFUSIVE REGIME

Abstract

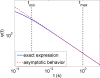
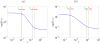
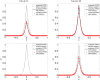
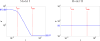
Subdiffusion has been proposed as an explanation of various kinetic phenomena inside living cells. In order to fascilitate large-scale computational studies of subdiffusive chemical processes, we extend a recently suggested mesoscopic model of subdiffusion into an accurate and consistent reaction-subdiffusion computational framework. Two different possible models of chemical reaction are revealed and some basic dynamic properties are derived. In certain cases those mesoscopic models have a direct interpretation at the macroscopic level as fractional partial differential equations in a bounded time interval. Through analysis and numerical experiments we estimate the macroscopic effects of reactions under subdiffusive mixing. The models display properties observed also in experiments: for a short time interval the behavior of the diffusion and the reaction is ordinary, in an intermediate interval the behavior is anomalous, and at long times the behavior is ordinary again.

Keywords: 35K57; 60J60; 92C45; anomalous kinetics; continuous-time random walk; fractional derivative; multistate reaction-diffusion system; subdiffusion.

Fig. 4.1

Section 4.1. Waiting time PDF (2.9) (blue solid line), and its asymptotic expansion (4.1) (red dotted line). The scales are logarithmic on both axes.

Fig. 5.1

Section 5.3. Comparison between the numerical values (circle) and the analytical values (solid line) of the concentration U = e^T u of A. (a): Set 1 of parameters at t₁ = 5 · 10⁻³ s, (b): Set 2 of parameters at t₂ = 1.5 · 10⁻¹ s.

Fig. 5.2

Section 5.3. Mean square displacement as a function of time. (a): Parameters set 1, (b): Parameters set 2. The scales are logarithmic on both axes.

Fig. 5.3

Section 5.4 Comparison between the numerical values (circles) and the analytical values (black line) of the conecntration U = e^T u of A at time t = 10⁻² s. Top: First run, bottom: Second run.

Fig. 5.4

Section 5.4 k′ in (4.22) in terms of time. Left: Model I, right: Model II. The scales are logarithmic on both axes.

Fig. 5.5

Section 5.4. Total amount of A (4.21) in terms of time. Upper: Model I, lower: Model II. The scale is logarithmic on the y axis.

Fig. 5.6

Section 5.5. Comparison between the numerical values (circles and triangles) and the analytical values (solid line and dashed line) of the concentration U = e^T u, V = e^T v of A and B at time t₁= 10⁻² s.

Fig. 5.7

Section 5.5. Numerical values of the concentration U = e^T u, V = e^T v of A and B at time t₂ = 10 s.

Fig. 5.8

Section 5.6. Numerical values of the concentration U = e^T u, V = e^T v, W = e^T w of A, B and C at time t₁ = 1 · 10⁻² s (top) and t₂ = 10 s (bottom).