Equivalence of internal and external mixture schemes of single scattering properties in vector radiative transfer

Abstract

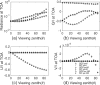
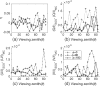
Polarized radiation fields in a turbid medium are influenced by single-scattering properties of scatterers. It is common that media contain two or more types of scatterers, which makes it essential to properly mix single-scattering properties of different types of scatterers in the vector radiative transfer theory. The vector radiative transfer solvers can be divided into two basic categories: the stochastic and deterministic methods. The stochastic method is basically the Monte Carlo method, which can handle scatterers with different scattering properties explicitly. This mixture scheme is called the external mixture scheme in this paper. The deterministic methods, however, can only deal with a single set of scattering properties in the smallest discretized spatial volume. The single-scattering properties of different types of scatterers have to be averaged before they are input to deterministic solvers. This second scheme is called the internal mixture scheme. The equivalence of these two different mixture schemes of scattering properties has not been demonstrated so far. In this paper, polarized radiation fields for several scattering media are solved using the Monte Carlo and successive order of scattering (SOS) methods and scattering media contain two types of scatterers: Rayleigh scatterers (molecules) and Mie scatterers (aerosols). The Monte Carlo and SOS methods employ external and internal mixture schemes of scatterers, respectively. It is found that the percentage differences between radiances solved by these two methods with different mixture schemes are of the order of 0.1%. The differences of Q/I, U/I, and V/I are of the order of 10^-5∼10^-4, where I, Q, U, and V are the Stokes parameters. Therefore, the equivalence between these two mixture schemes is confirmed to the accuracy level of the radiative transfer numerical benchmarks. This result provides important guidelines for many radiative transfer applications that involve the mixture of different scattering and absorptive particles.

Fig. 1

Diagram of the solar and viewing angle geometry. The local normal vector and the Sun define the principal plane. Two detectors are shown: one is at the TOA, measuring the reflected Stokes parameters; the other is at the BOA, measuring the transmitted Stokes parameters.

Fig. 2

Radiance I and Q/I, U/I, and V/I at TOA for the conservative case. The azimuth angle ϕ legend in Fig. 2(d) applies to all four subplots in Fig. 2. The solar zenith angle is 60°.

Fig. 3

Radiance percentage difference between the SOS and MC methods at TOA for the conservative case shown as in Fig. 2. Also shown are the Q/I, U/I, and V/I differences between the SOS and MC methods. The azimuth angle ϕ legend in Fig. 3(d) applies to all four subplots in Fig. 3.

Fig. 4

Same as Fig. 2 except that these are for the BOA.

Fig. 5

Same as Fig. 3 except that these are for the BOA.

Fig. 6

Radiation field at TOA for the nonconservative (absorbing) case.

Fig. 7

Differences between the radiation field calculated by the two methods for case shown in Fig. 6.

Fig. 8

Radiation field at the BOA for the nonconservative case.

Fig. 9

Difference between the radiation field calculated by the two methods at the BOA for the nonconservative case.