Classical Statistics and Statistical Learning in Imaging Neuroscience

Abstract

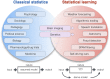
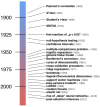
Brain-imaging research has predominantly generated insight by means of classical statistics, including regression-type analyses and null-hypothesis testing using t-test and ANOVA. Throughout recent years, statistical learning methods enjoy increasing popularity especially for applications in rich and complex data, including cross-validated out-of-sample prediction using pattern classification and sparsity-inducing regression. This concept paper discusses the implications of inferential justifications and algorithmic methodologies in common data analysis scenarios in neuroimaging. It is retraced how classical statistics and statistical learning originated from different historical contexts, build on different theoretical foundations, make different assumptions, and evaluate different outcome metrics to permit differently nuanced conclusions. The present considerations should help reduce current confusion between model-driven classical hypothesis testing and data-driven learning algorithms for investigating the brain with imaging techniques.

Keywords: Rosetta Stone; data science; epistemology; machine learning; neuroimaging; p-value; statistical inference.

Figure 1

Application areas of two statistical paradigms. Lists examples of research domains which apply relatively more classical statistics (blue) or learning algorithms (red). The co-occurrence of increased computational resources, growing data repositories, and improving pattern-learning techniques have initiated a shift toward less hypothesis-driven and more algorithmic methodologies. As a broad intuition, researchers in the empirical sciences on the left tend to use statistics to evaluate a pre-assumed model on the data. Researchers in the application domains on the right tend to derive a model directly from the data: A new function with potentially many parameters is created that can predict the output from the input alone without explicit programming model. One of the key differences becomes apparent when thinking of the neurobiological phenomenon under study as a black box (Breiman, 2001). ClSt typically aims at modeling the black box by making a set of formal assumptions about its content, such as the nature of the signal distribution. Gaussian distributional assumptions have been very useful in many instances to enhance mathematical convenience and, hence, computational tractability. Instead, StLe takes a brute-force approach to model the output of the black box (e.g., tell healthy and schizophrenic people apart) from its input (e.g., volumetric brain measurements) while making a possible minimum of assumptions (Abu-Mostafa et al., 2012). In ClSt the stochastic processes that generated the data is therefore treated as partly known, whereas in StLe the phenomenon is treated as complex, largely unknown, and partly unknowable.

Figure 2

Developments in the history of classical statistics and statistical learning. Examples of important inventions in statistical methodology. Roughly, a number of statistical methods taught in today's textbooks in psychology and medicine have emerged in the first half of the twentieth century (blue). Instead, many algorithmic techniques and procedures have emerged in the second half of the twentieth century (red). “The postwar era witnessed a massive expansion of statistical methodology, responding to the data-driven demands of modern scientific technology.” (Efron and Hastie, 2016).

Figure 3

Key differences in the modeling philosophy of classical statistics and statistical learning. Ten modeling intuitions that tend to be relatively more characteristic for classical statistical methods (blue) or pattern-learning methods (red). In comparison to ClSt, StLe “is essentially a form of applied statistics with increased emphasis on the use of computers to statistically estimate complicated functions and a decreased emphasis on proving confidence intervals around these functions” (Goodfellow et al., 2016). Broadly, ClSt tends to be more analytical by imposing mathematical rigor on the phenomenon, whereas StLe tends to be more heuristic by finding useful approximations. In practice, ClSt is probably more often applied to experimental data, where a set of target variables are systematically controlled by the investigator and the brain system under studied has been subject to experimental perturbation. Instead, StLe is probably more often applied to observational data without such structured influence and where the studied system has been left unperturbed. ClSt fully specifies the statistical model at the beginning of the investigation, whereas in StLe there is a bigger emphasis on models that can flexibly adapt to the data (e.g., learning algorithms creating decision trees).

Figure 4

Key concepts in classical statistics and statistical learning. Schematic with statistical notions that are relatively more associated with classical statistical methods (left column) or pattern-learning methods (right column). As there is a smooth transition between the classical statistical toolkit and learning algorithms, some notions may be closely associated with both statistical cultures (middle column).

Figure 5

Key differences between measuring outcomes in classical statistics and statistical learning. Ten intuitions on quantifying statistical modeling outcomes that tend to be relatively more true for classical statistical methods (blue) or pattern-learning methods (red). ClSt typically yields point estimates and interval estimates (e.g., p-values, variances, confidence intervals), whereas StLe frequently outputs a function or a program that can yield point and interval estimates on new observations (e.g., the k-means centroids or a trained classifier's decision function can be applied to new data). In many cases, classical inference is a judgment about an entire data sample, whereas a trained predictive model can obtain quantitative answers from a single data point.