Individual mobility promotes punishment in evolutionary public goods games

Abstract

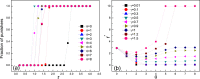
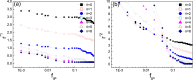
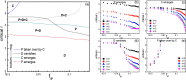
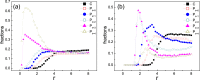
In explaining the pressing issue in biology and social sciences how cooperation emerges in a population of self-interested individuals, researchers recently pay intensive attentions to the role altruistic punishment plays. However, as higher-order cooperators, survival of punishers is puzzling due to their extra cost in regulating norm violators. Previous works have highlighted the importance of individual mobility in promoting cooperation. Yet its effect on punishers remains to be explored. In this work we incorporate this feature into modeling the behavior of punishers, who are endowed with a choice between leaving current place or staying and punishing defectors. Results indicate that optimal mobility level of punishers is closely related to the cost of punishing. For considerably large cost, there exists medium tendency of migration which favors the survival of punishers. This holds for both the direct competition between punishers and defectors and the case where cooperators are involved, and can also be observed when various types of punishers with different mobility tendencies fight against defectors simultaneously. For cheap punishment, mobility does not provide with punishers more advantage even when they are initially rare. We hope our work provide more insight into understanding the role individual mobility plays in promoting public cooperation.

Figure 1

(a) Fraction of punishers as a function of enhancement factor $r$ for different values of threshold of migration $\theta$ with punishment cost $\gamma =0.7$ and intensity $\beta =1$. Notably, a medium value of $\theta$ favors punishers most under this circumstance. (b) Critical value of enhancement factor $r^{⁎}$ above which punishers dominate as a function of threshold of migration $\theta$ for different values of punishment cost $\gamma$ when $\beta =1$. Lower $r^{⁎}$ implies a more favorable environment for punishers. Note that for low punishment cost, to stay still and always to punish is a best choice. While for larger punishment cost, there exists medium value of $\theta$ that is optimal. Initially equal fractions 0.5 of punishers and defectors are randomly distributed among the population. Population density is $\rho =0.5$.

Figure 2

Fraction of punishers in dependence of punishing cost $\gamma$ and punishing intensity $\beta$ in the contour form when population are composed of D and P. Different panels correspond to different threshold to migrate $\theta =\mathrm{1,\; 2,\; 3,\; 4}$, respectively. The case for $\theta =0$ is not shown where defectors dominate for the whole given parameter plane. Initial fraction of P and D are both 0.5. Other parameters: $r=2$, and $\rho =0.5$.

Figure 3

Critical value of $r$ as a function of initial fraction of punishers $f_{IP}$. (a) Critical value of enhancement factor $r^{\mathrm{⁎1}}$, above which punishers emerge dependent on $f_{IP}$ for different values of $\theta$. (b) Critical value of enhancement factor $r^{\mathrm{⁎2}}$, above which punishers dominate the population dependent on $f_{IP}$ for different values of $\theta$. The criterion for emergence and dominance of punishers are that the average stationary fractions reach 0.01 and 0.99, respectively. Other parameters: $\gamma =0.3$, $\beta =1$, and $\rho =0.5$.

Figure 4

(a) Fractions of C, D, and P as functions of enhancement factor $r$. (b) Fraction of P as a function of $r$ for different values of $\theta$ when $\gamma =0.7$. (c) Fraction of P as a function of $\theta$ for different values of punishing cost $\gamma$ s when $r=3$. Population density is $\rho =0.5$.

Figure 5

Fraction of punishers in dependence of punishing cost $\gamma$ and punishing intensity $\beta$ in the contour form when population are composed of C, D, and P. The first row corresponds to $r=2$ while the second row $r=3$. Different columns correspond to different thresholds to migrate $\theta =\mathrm{1,\; 2,\; 3,\; 4}$. The case for $\theta =0$ is not shown where defectors dominate for the whole given parameter area of $\gamma$ and $\beta$. Insects show the fraction of cooperators for the same parameter region as punishers.Initial fraction of C and P are both 0.25, and the rest D 0.5. Population density is $\rho =0.5$.

Figure 6

(a) Phase diagram for the stationary composition of population (C, D, and P) dependent on the initial fraction of punishers $f_{IP}$ and enhancement factor $r$ in the case of $\theta =0$. Legends indicates the crucial lines above which particular events occur as $r$ increases. Dashed line denote the $r$ values where equal percentage of Cs and Ps are obtained. As the initial fraction of punishers varies, the total percentage of initial cooperators and punishers remains 50%, with the remainder 50% being defectors. The influences of $\theta$ on each of the four lines shown in (a) are illustrated respectively in (b–e). For panels (a–e), the punishment cost is $\gamma =0.3$ and intensity is $\beta =1$. Population density is $\rho =0.5$.

Figure 7

Fractions of different punisher classes and pure cooperators in the final state in dependence of enhancement factor $r$ when they start fighting with defectors simultaneously. Initially defectors take up 50% of the whole population and the rest are occupied by equal percentage of all these 6 types of individuals. Subscripts $\theta =\mathrm{0,\; 1...4}$ of P indicates the threshold of this type of P to migrate without punishing. Panel (a) corresponds to relatively low punishing cost $\gamma =0.3$ while Panel (b) high cost $\gamma =0.9$. Other parameters: $\beta =1$, and $\rho =0.5$. Data are obtained by averaging over 500 independent simulation runs.