Pendular energy transduction within the step during human walking on slopes at different speeds

Abstract

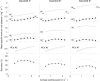
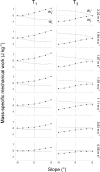
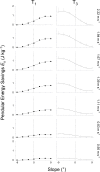
When ascending (descending) a slope, positive (negative) work must be performed to overcome changes in gravitational potential energy at the center of body mass (COM). This modifies the pendulum-like behavior of walking. The aim of this study is to analyze how energy exchange and mechanical work done vary within a step across slopes and speeds. Ten subjects walked on an instrumented treadmill at different slopes (from -9° to 9°), and speeds (between 0.56 and 2.22 m s-1). From the ground reaction forces, we evaluated energy of the COM, recovery (i.e. the potential-kinetic energy transduction) and pendular energy savings (i.e. the theoretical reduction in work due to this recovered energy) throughout the step. When walking uphill as compared to level, pendular energy savings increase during the first part of stance (when the COM is lifted) and decreases during the second part. Conversely in downhill walking, pendular energy savings decrease during the first part of stance and increase during the second part (when the COM is lowered). In uphill and downhill walking, the main phase of external work occurs around double support. Uphill, the positive work phase is extended during the beginning of single support to raise the body. Downhill, the negative work phase starts before double support, slowing the downward velocity of the body. Changes of the pendulum-like behavior as a function of slope can be illustrated by tilting the 'classical compass model' backwards (uphill) or forwards (downhill).

Fig 1. Typical time-traces of a subject walking at ~0.83 m s^-1 (3 km h^-1) on a -9° slope (left column), on the level (middle column) and on a +9° slope (right column).

Top panels: Mechanical energy-time curves of the COM during a stride. Strides are delimited by the maximal fore-aft velocity of the COM when the right foot is in front. The upper curve (E_k) refers to the kinetic energy of the COM, the middle curve (E_p) to its gravitational potential energy and the bottom curve (E_ext = E_k + E_p) to the total energy of the COM. The grey zones correspond to the double contact periods (starting at right or left foot contact -RFC or LFC- and ending at right or left toe-off -RTO or LTO). The vertical interrupted lines correspond to the extrema of the E_k and E_p curves. Note that these energy-time curves are qualitatively similar to the one obtained by Gottschall and Kram (2006). Middle panels: Instantaneous recovery (r(t), Eq 3) at each instant t of the stride. The recovery r(t) varies form 0% when the E_k and E_p curves are in phase, to 100% when the decrease of one curve equals the increase of the other. When r(t) = 100%, E_ext is constant and no external work is done to move the COM relative to the surroundings. Lower panels: Rate of pendular energy savings ($\dot{e}\left(t\right)$, Eq 4) at each instant t of the stride. These curves represent the rate at which energy is economized through the transformation of kinetic into potential energy (or vice versa). Time is expressed as a percentage of the stride period. Tracings were recorded on a male subject (height: 1.82 m, body mass: 74.3 kg, age: 24.7 y.o.). Lower schemas: The schemas represent the 'compass walking' model with the approximate division of one step of the stride into the four phases T1, T2, T3 & T4 (see methods) during downhill, level and uphill walking. During T1, E_k decreases while E_p increases, during T3 E_k increases while E_p decreases. During T2 and T4, both E_k and E_p increase or decrease (arrows).

Fig 2. Typical time-traces of a subject walking at ~1.39 m s^-1 (5 km h^-1) on a -9° slope (left column), on the level (middle column) and on a +9° slope (right column).

Same indications as in Fig 1.

Fig 3. Typical time-traces of a subject walking at ~1.94 m s^-1 (7 km h^-1) on a -9° slope (left column), on the level (middle column) and on a +9° slope (right column).

Same indications as in Fig 1.

Fig 4. Mass-normalized work per unit distance and recovery over the step as a function of speed and slope while walking uphill.

Three top rows: For each slope, the mass-normalized positive (closed symbols, superscript +) and negative (open symbols, superscript -) mechanical work done per unit distance is given as a function of walking speed. Top row: $W_{\mathrm{ext}}^{+}$ and $W_{\mathrm{ext}}^{-}$ are the positive and negative external work estimated to move the COM through its observed trajectory, relative to the surroundings. The horizontal dotted line (W_m) represents the minimal work necessary to overcome the change in gravitational potential energy. Second row: $W_{\mathrm{v}}^{+}$ and $W_{\mathrm{v}}^{-}$ are the positive and negative work due to the changes in E_p+E_kv vs. time curve. Third row: $W_{\mathrm{f}}^{+}$ and $W_{\mathrm{f}}^{-}$ are the positive and negative work due to the changes in E_kf vs. time curve (since the average speed is constant, $W_{\mathrm{f}}^{+}=W_{\mathrm{f}}^{-}$). Because $W_{\mathrm{l}}^{+}$ and $W_{\mathrm{l}}^{-}$ represents less than 1.5% of $W_{\mathrm{ext}}^{+}$ and $W_{\mathrm{ext}}^{-}$, it is not presented in this figure. Bottom row: The bottom panels present the recovery calculated over the whole step (R_step, Eq 2) as a function of speed. In each panel, symbols and bars represent the "grand mean" of the subjects (see Methods and Table 1) and the standard deviations (when the length of the bar exceeds the size of the symbol). The continuous lines were drawn through the experimental data (polynomial function, Kaleidagraph 4.5). The dashed lines represent the work done or the recovery during walking on the level; these lines were also drawn through the experimental data (polynomial function, Kaleidagraph 4.5).

Fig 5. Mass-specific work per unit distance and recovery over the step as a function of speed and slope while walking downhill.

Same indications as in Fig 4.

Fig 6. Duration of the four phases of the step as a function of slope at each speed.

In each panel, the time is expressed as a percentage of the step duration: 0% and 100% (vertical interrupted lines) correspond to the moments at which the fore-aft velocity of the COM is maximal. The closed circles correspond to the instant of E_k,max, the open circles to E_k,min, the closed squares to E_p,max, and the open squares to E_p,min. The grey zones correspond to the phases during which E_k can be transformed into E_p (T1) and vice versa (T3). The white zones correspond to the phases where the curves are in phase. Symbols and bars represent the "grand mean" of all subjects (Table 1) at a given speed and slope and the standard deviations (when the length of the bar exceeds the size of the symbol).

Fig 7. Change in the kinetic and potential energy during the periods T1 and T3 as a function of slope at each speed.

At each speed, the left panel presents the increments of the E_p curve ($W_{\mathrm{p}}^{+}$, closed circles) and the decrements of the E_k curve ($W_{\mathrm{k}}^{-}$, open circles) during the period T1 whereas the right panel presents the decrements of the E_p curve ($W_{\mathrm{p}}^{-}$, closed circles) and the increments of the E_k curve ($W_{\mathrm{k}}^{+}$, open circles) over the period T3. Other indications as in Fig 4.

Fig 8. Average of the instantaneous recovery (R_avg) over the periods T1 and T3 as a function of slope at each speed.

At each speed, the left panel (closed circles) presents R_avg (see Methods) over the period T1 whereas the right panel (open circles) presents R_avg over the period T3. Other indications as in Fig 4.

Fig 9. Pendular energy savings (E_s) over the periods T1 and T3 as a function of slope at each speed.

At each speed, the left panel (closed circles) presents E_s (see Methods) over the period T1 whereas the right panel (open circles) presents E_s over the period T3. Other indications as in Fig 4.

Fig 10. External work done during the four phases of the step as a function of slope at each speed.

At each speed, the mass-normalized external work is presented during the four phases of the step as a function of the slope. In each panel, the closed and open circles correspond respectively to the positive and negative external work done during that phase. Other indications as in Fig 4.