Quantum phase slips: from condensed matter to ultracold quantum gases

Abstract

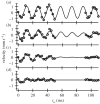
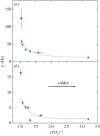
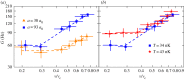
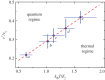
Quantum phase slips (QPS) are the primary excitations in one-dimensional superfluids and superconductors at low temperatures. They have been well characterized in most condensed-matter systems, and signatures of their existence have been recently observed in superfluids based on quantum gases too. In this review, we briefly summarize the main results obtained on the investigation of phase slips from superconductors to quantum gases. In particular, we focus our attention on recent experimental results of the dissipation in one-dimensional Bose superfluids flowing along a shallow periodic potential, which show signatures of QPS.This article is part of the themed issue 'Breakdown of ergodicity in quantum systems: from solids to synthetic matter'.

Keywords: dissipation; quantum phase slips; superfluids; transport.

Figure 1.

From thermal phase slips to QPS in nanowires. Resistance in In wires as a function of the temperature, for three different values of the wire diameter. Solid lines are the fits with a thermal activation mechanism, while dashed curves include both thermal and quantum contributions. Figure adapted from [2].

Figure 2.

Increased role of thermal and quantum fluctuations in one-dimensional quantum gases. Damped oscillations of a ⁸⁷Rb one-dimensional gas in an optical lattice, for different lattice depths, expressed in units of the atomic recoil energy, s=V ₀/(h²/2mλ²): (a) s=0, (b) s=0.25, (c) s=0.5, (d) s=2. Figure adapted from [45].

Figure 3.

Onset of a temperature-independent phase slip regime. Temperature dependence of the damping rate γ, measured in oscillation of a ⁸⁷Rb Bose–Einstein condensate in a three-dimensional optical lattice for two values of the lattice depth: (a) s=6, (b) s=2. Figure adapted from [48]. (Online version in colour.)

Figure 4.

Detecting the dynamical instability and the Mott insulator transition. (a) Time evolution of the momentum distribution peak p at s=2 for different values of scattering length. The solid lines are the theoretical damped oscillation fitting the data for p<p_c before the dynamical instability sets in. The green stars mark the critical momentum p_c. (b) Critical momentum p_c versus scattering length for two lattice depth: s=4 (red squares) and s=2 (black circles). A piecewise fit (solid lines) determines the critical values for the superfluid–Mott insulator transition (empty circles) for n=1. Figure adapted from [52]. (Online version in colour.)

Figure 5.

Onset of velocity-dependent dissipation. (a) Damping rate G plotted as a function of the maximum velocity v normalized to the critical velocity v_c, for two interaction strengths and constant temperature. (b) G as a function of v/v_c for two different temperatures and approximately constant interaction energy. The lines are fits to measure the crossover velocity v*. Figure adapted from [52]. (Online version in colour.)

Figure 6.

Experimental diagram of thermal and quantum dissipation regimes. Crossover velocity v*/v_c as a function of k_BT/E_j. The individual datapoints have been taken for different temperatures and interaction energies. The dashed line apparently separates the thermal and the quantum regimes for phase slips. Figure adapted from [52]. (Online version in colour.)