Numerical Hydrodynamics in General Relativity
- PMID: 29104452
- PMCID: PMC5660627
- DOI: 10.12942/lrr-2003-4
Numerical Hydrodynamics in General Relativity
Abstract
The current status of numerical solutions for the equations of ideal general relativistic hydrodynamics is reviewed. With respect to an earlier version of the article, the present update provides additional information on numerical schemes, and extends the discussion of astrophysical simulations in general relativistic hydrodynamics. Different formulations of the equations are presented, with special mention of conservative and hyperbolic formulations well-adapted to advanced numerical methods. A large sample of available numerical schemes is discussed, paying particular attention to solution procedures based on schemes exploiting the characteristic structure of the equations through linearized Riemann solvers. A comprehensive summary of astrophysical simulations in strong gravitational fields is presented. These include gravitational collapse, accretion onto black holes, and hydrodynamical evolutions of neutron stars. The material contained in these sections highlights the numerical challenges of various representative simulations. It also follows, to some extent, the chronological development of the field, concerning advances on the formulation of the gravitational field and hydrodynamic equations and the numerical methodology designed to solve them.
Electronic supplementary material: Supplementary material is available for this article at 10.12942/lrr-2003-4.
Figures


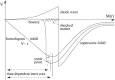


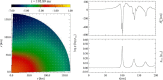
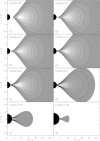


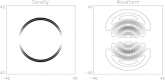


References
-
- Abramowicz M, Jaroszynski M, Sikora M. Relativistic, accreting disks. Astron. Astrophys. 1978;63:221–224.
-
- Abramowicz MA, Calvani M, Nobili L. Runaway instability in accretion disks orbiting black holes. Nature. 1983;302:597–599. doi: 10.1038/302597a0. - DOI
-
- Abramowicz MA, Czerny B, Lasota JP, Szuszkiewicz E. Slim accretion disks. Astrophys. J. 1988;332:646–658. doi: 10.1086/166683. - DOI
-
- Alcubierre M, Allen G, Brügmann B, Dramlitsch T, Font JA, Papadopoulos P, Seidel E, Stergioulas N, Suen W-M, Takahashi R. Towards a stable numerical evolution of strongly gravitating systems in general relativity: The conformal treatments. Phys. Rev. D. 2000;62:044034–1-044034-16. doi: 10.1103/PhysRevD.62.044034. - DOI
-
- Alcubierre M, Allen G, Brügmann B, Seidel E, Suen W-M. Towards an understanding of the stability properties of the 3+1 evolution equations in general relativity. Phys. Rev. D. 2000;62:124011–1-124011-15. doi: 10.1103/PhysRevD.62.124011. - DOI
Publication types
LinkOut - more resources
Full Text Sources
