Correlating cell shape and cellular stress in motile confluent tissues

Abstract

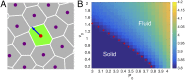
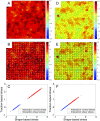
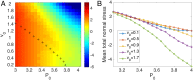
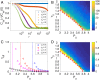
Collective cell migration is a highly regulated process involved in wound healing, cancer metastasis, and morphogenesis. Mechanical interactions among cells provide an important regulatory mechanism to coordinate such collective motion. Using a self-propelled Voronoi (SPV) model that links cell mechanics to cell shape and cell motility, we formulate a generalized mechanical inference method to obtain the spatiotemporal distribution of cellular stresses from measured traction forces in motile tissues and show that such traction-based stresses match those calculated from instantaneous cell shapes. We additionally use stress information to characterize the rheological properties of the tissue. We identify a motility-induced swim stress that adds to the interaction stress to determine the global contractility or extensibility of epithelia. We further show that the temporal correlation of the interaction shear stress determines an effective viscosity of the tissue that diverges at the liquid-solid transition, suggesting the possibility of extracting rheological information directly from traction data.

Keywords: cell shape; cell stress; phase transition; self-propelled; vertex model.

Fig. 1.

(A) Illustration of the SPV model, where cells are represented by polygons obtained via a Voronoi tessellation of initially random cell positions, with a self-propulsion force applied at each cell position. (B) Phase diagram in the $(P_0,v_0)$ plane based on the value of the shape parameter $q$ (color scale), with the phase boundary (red crosses) determined by $q=3.813$.

Fig. 2.

Comparison of shape-based and coarse-grained traction-based stress. (A–C) Solid state at $v_0=0.5$, $P_0=3.3$. (D–F) Liquid state at $v_0=0.5$, $P_0=3.8$. (A and D) Interaction normal stress ${\sigma }_n^{(i)int}$ calculated from the instantaneous cell shapes obtained from Eqs. 3a and 7. Red denotes positive (contractile) stress and blue negative (extensile) stress. (B and E) Interaction normal stress ${\sigma }_n^{(i)int}$ calculated using the coarse-grained traction-based mechanical inference by inverting Eq. 9 and using Eq. 3a. The arrows denote the traction forces. (C and F) The coarse-grained traction-based mechanical inference is validated by plotting the traction-based stress against the shape-based stress in the solid (C) and in the liquid (F) state. The data are for $400$ cells in a square box of side $L=20$ with $D_r=0.1$ and with periodic boundary condition.

Fig. 3.

Mean total normal stress. (A) Heat map of the mean total normal stress of the tissue in the $(v_0,P_0)$ plane. The black crosses outline the solid–liquid phase boundary determined by $q=3.813$. Red indicates contractile stress and blue extensile stress. (B) Mean total normal stress as a function of $P_0$ at various $v_0$, showing a change in sign deep in the liquid state ($400$ cells for $T=\mathrm{1,000}$ and $D_r=0.1$ with periodic boundary condition).

Fig. 4.

Time autocorrelation of interaction shear stress and effective tissue viscosity. (A) Time autocorrelation function of the mean interaction shear stress for $P_0=3.45$ at various $v_0$. (B and D) Heat maps of the correlation time ${\tau }_m$ (B) and of the effective viscosity (D). The red crosses denote the liquid–solid phase transition boundary determined by $q=3.813$. The white region corresponds to regions where correlation time ${\tau }_m$ and effective viscosity ${\eta }_{\mathrm{𝑒𝑓𝑓}}$ diverge. Note that these regions largely coincide with the solid regime. (C) The effective viscosity as a function of $P_0$ at various $v_0$. The dashed lines correspond to the critical $P_0$ where the liquid–solid phase transition occurs. All results are for $100$ cells, $D_r=1$, and $T=\mathrm{40,000}$ with periodic boundary condition.