A coupled-oscillator model of olfactory bulb gamma oscillations
- PMID: 29140973
- PMCID: PMC5706731
- DOI: 10.1371/journal.pcbi.1005760
A coupled-oscillator model of olfactory bulb gamma oscillations
Abstract
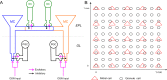
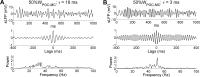
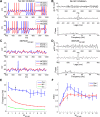
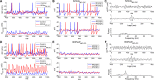
The olfactory bulb transforms not only the information content of the primary sensory representation, but also its underlying coding metric. High-variance, slow-timescale primary odor representations are transformed by bulbar circuitry into secondary representations based on principal neuron spike patterns that are tightly regulated in time. This emergent fast timescale for signaling is reflected in gamma-band local field potentials, presumably serving to efficiently integrate olfactory sensory information into the temporally regulated information networks of the central nervous system. To understand this transformation and its integration with interareal coordination mechanisms requires that we understand its fundamental dynamical principles. Using a biophysically explicit, multiscale model of olfactory bulb circuitry, we here demonstrate that an inhibition-coupled intrinsic oscillator framework, pyramidal resonance interneuron network gamma (PRING), best captures the diversity of physiological properties exhibited by the olfactory bulb. Most importantly, these properties include global zero-phase synchronization in the gamma band, the phase-restriction of informative spikes in principal neurons with respect to this common clock, and the robustness of this synchronous oscillatory regime to multiple challenging conditions observed in the biological system. These conditions include substantial heterogeneities in afferent activation levels and excitatory synaptic weights, high levels of uncorrelated background activity among principal neurons, and spike frequencies in both principal neurons and interneurons that are irregular in time and much lower than the gamma frequency. This coupled cellular oscillator architecture permits stable and replicable ensemble responses to diverse sensory stimuli under various external conditions as well as to changes in network parameters arising from learning-dependent synaptic plasticity.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures











Similar articles
-
Coherent olfactory bulb gamma oscillations arise from coupling independent columnar oscillators.J Neurophysiol. 2024 Mar 1;131(3):492-508. doi: 10.1152/jn.00361.2023. Epub 2024 Jan 24. J Neurophysiol. 2024. PMID: 38264784 Free PMC article.
-
Circuit properties generating gamma oscillations in a network model of the olfactory bulb.J Neurophysiol. 2006 Apr;95(4):2678-91. doi: 10.1152/jn.01141.2005. Epub 2005 Dec 28. J Neurophysiol. 2006. PMID: 16381804
-
Interplay between local GABAergic interneurons and relay neurons generates gamma oscillations in the rat olfactory bulb.J Neurosci. 2004 May 5;24(18):4382-92. doi: 10.1523/JNEUROSCI.5570-03.2004. J Neurosci. 2004. PMID: 15128852 Free PMC article.
-
Adjusting neurophysiological computations in the adult olfactory bulb.Semin Cell Dev Biol. 2006 Aug;17(4):443-53. doi: 10.1016/j.semcdb.2006.04.011. Epub 2006 May 5. Semin Cell Dev Biol. 2006. PMID: 16757194 Review.
-
Centrifugal drive onto local inhibitory interneurons of the olfactory bulb.Ann N Y Acad Sci. 2009 Jul;1170:239-54. doi: 10.1111/j.1749-6632.2009.03913.x. Ann N Y Acad Sci. 2009. PMID: 19686142 Review.
Cited by
-
Odor-evoked increases in olfactory bulb mitral cell spiking variability.iScience. 2021 Aug 4;24(9):102946. doi: 10.1016/j.isci.2021.102946. eCollection 2021 Sep 24. iScience. 2021. PMID: 34485855 Free PMC article.
-
Generalized Cross-Frequency Decomposition: A Method for the Extraction of Neuronal Components Coupled at Different Frequencies.Front Neuroinform. 2018 Oct 18;12:72. doi: 10.3389/fninf.2018.00072. eCollection 2018. Front Neuroinform. 2018. PMID: 30405385 Free PMC article.
-
Differences in olfactory bulb mitral cell spiking with ortho- and retronasal stimulation revealed by data-driven models.PLoS Comput Biol. 2021 Sep 20;17(9):e1009169. doi: 10.1371/journal.pcbi.1009169. eCollection 2021 Sep. PLoS Comput Biol. 2021. PMID: 34543261 Free PMC article.
-
Heterogeneous quantization regularizes spiking neural network activity.Sci Rep. 2025 Apr 23;15(1):14045. doi: 10.1038/s41598-025-96223-z. Sci Rep. 2025. PMID: 40268966 Free PMC article.
-
Generative Biophysical Modeling of Dynamical Networks in the Olfactory System.Methods Mol Biol. 2018;1820:265-288. doi: 10.1007/978-1-4939-8609-5_20. Methods Mol Biol. 2018. PMID: 29884952 Free PMC article.
References
-
- Shepherd GM, Chen WR, Greer CA. Olfactory bulb In: The Synaptic Organization of the Brain (5th ed.), edited by Shepherd GM. Oxford, UK: Oxford Univ. Press; 2004. pp. 165–216.
-
- Cleland TA. Construction of odor representations by olfactory bulb microcircuits. Prog Brain Res. 2014; 208:177–203. doi: 10.1016/B978-0-444-63350-7.00007-3 - DOI - PubMed
-
- Kay LM, Lazzara P. How global are olfactory bulb oscillations? J Neurophysiol. 2010; 104(3):1768–1773. doi: 10.1152/jn.00478.2010 - DOI - PMC - PubMed
-
- Freeman WJ, Viana Di Prisco G. Relation of olfactory EEG to behavior: time series analysis. Behav Neurosci. 1986; 100(5):753–763. - PubMed
-
- Freeman WJ, Baird B. Relation of olfactory EEG to behavior: spatial analysis. Behav Neurosci. 1987; 101(3):393–408. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

