Modelling the effects of phylogeny and body size on within-host pathogen replication and immune response

Abstract

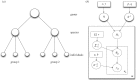
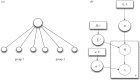
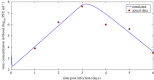
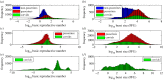
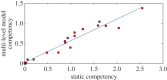
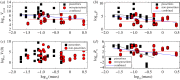
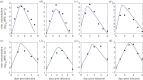
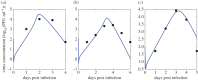
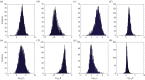
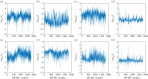
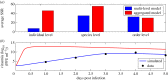
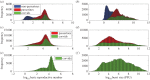
Understanding how quickly pathogens replicate and how quickly the immune system responds is important for predicting the epidemic spread of emerging pathogens. Host body size, through its correlation with metabolic rates, is theoretically predicted to impact pathogen replication rates and immune system response rates. Here, we use mathematical models of viral time courses from multiple species of birds infected by a generalist pathogen (West Nile Virus; WNV) to test more thoroughly how disease progression and immune response depend on mass and host phylogeny. We use hierarchical Bayesian models coupled with nonlinear dynamical models of disease dynamics to incorporate the hierarchical nature of host phylogeny. Our analysis suggests an important role for both host phylogeny and species mass in determining factors important for viral spread such as the basic reproductive number, WNV production rate, peak viraemia in blood and competency of a host to infect mosquitoes. Our model is based on a principled analysis and gives a quantitative prediction for key epidemiological determinants and how they vary with species mass and phylogeny. This leads to new hypotheses about the mechanisms that cause certain taxonomic groups to have higher viraemia. For example, our models suggest that higher viral burst sizes cause corvids to have higher levels of viraemia and that the cellular rate of virus production is lower in larger species. We derive a metric of competency of a host to infect disease vectors and thereby sustain the disease between hosts. This suggests that smaller passerine species are highly competent at spreading the disease compared with larger non-passerine species. Our models lend mechanistic insight into why some species (smaller passerine species) are pathogen reservoirs and some (larger non-passerine species) are potentially dead-end hosts for WNV. Our techniques give insights into the role of body mass and host phylogeny in the spread of WNV and potentially other zoonotic diseases. The major contribution of this work is a computational framework for infectious disease modelling at the within-host level that leverages data from multiple species. This is likely to be of interest to modellers of infectious diseases that jump species barriers and infect multiple species. Our method can be used to computationally determine the competency of a host to infect mosquitoes that will sustain WNV and other zoonotic diseases. We find that smaller passerine species are more competent in spreading the disease than larger non-passerine species. This suggests the role of host phylogeny as an important determinant of within-host pathogen replication. Ultimately, we view our work as an important step in linking within-host viral dynamics models to between-host models that determine spread of infectious disease between different hosts.

Keywords: Flavivirus; West Nile Virus; disease modelling; emerging diseases; hierarchical Bayesian models; mathematical modelling; zoonotic diseases; modelling diseases.

Figure 1.

(a) Multi-level hierarchical model with two groups. Each group has three individuals. Also shown are the genus, species and individual levels. (b) Plate diagram for the multi-level hierarchical model. The plate denotes iteration of parameters and the number enclosed in the plate shows the number of iterations.

Figure 2.

(a) Aggregated model with two groups combined. Each group has three individuals. Also shown are the genus, species and individual levels. (b) Plate diagram for the aggregated model. The plate denotes iteration of parameters and the number in the plate shows the number of iterations.

Figure 3.

A sample ODE prediction for virus concentration (in log₁₀ PFU ml⁻¹) over time post infection (blue) and experimental data on virus concentration (red). Data show viraemia of great-horned owls from [13]. (Online version in colour.)

Figure 4.

Posterior distribution of log₁₀ R₀ and burst size (log₁₀ p/δ) for the multi-level model (target cell limited model). (a,b) Multi-level model with all passerines (red), corvids (green) and non-passerines (blue). (c,d) Multi-level model with only passerines (red) and corvids (green). (e,f) Multi-level model with only corvids (green).

Figure 5.

Correlation between multi-level model predicted competency and competency from Komar et al. [13] assuming static viraemia (r² = 0.94, slope = 0.54, p-value = 1×10⁻⁶). (Online version in colour.)

Figure 6.

Scaling of biologically relevant quantities with host mass for the multi-level model: passerines (black square and black regression line, non-passerines (red circle and red regression line) and all combined (blue regression line). (a) Peak viraemia (V_p), slope =−0.82, p-value = 0.06, r² = 0.04. (b) WNV production rate (p), slope =−1.1, p-value = 0.002, r² = 0.11. (c) Inoculated density of virions (V₀), p-value = 0.35. (d) R₀, slope =−1.3, p-value = 0.006, r² = 0.09. (Online version in colour.)

Figure 7.

Scaling of immune response parameters with host mass for the multi-level model with immune response: passerines (black square) and non-passerines (red circle). (a) Rate of adaptive immune system mediated virus neutralization (ρ, PRNT⁻¹₅₀ d⁻¹). (b) Time of initiation of IgM response (t_i, days) (combined and each group separately are non-significant). (Online version in colour.)

Figure 8.

Predictions from the ODE model given by equations (3.2)–(3.5) for plasma virus concentration (in log₁₀ PFU ml⁻¹) over time post infection (blue) and experimental data on virus concentration (black). Parameters used are the mean for each species from the multi-level model. Data show the viraemia of the following species from [13]: (a–h) American crow, American robin, red-winged blackbird, black-billed magpie, house finch, house sparrow, mallard and mourning dove, respectively. (Online version in colour.)

Figure 9.

Predictions from the ODE model given by equations (3.2)–(3.5) for plasma virus concentration (in log₁₀ PFU ml⁻¹) over time post infection (blue) and experimental data on virus concentration (black). Parameters used are the mean for each species from the multi-level model. Data show the viraemia of the following species from [13]: (a–h) ring-billed gull, great-horned owl, American kestrel, killdeer, northern bobwhite, northern flicker, rock dove and American coot, respectively. (Online version in colour.)

Figure 10.

Predictions from the ODE model given by equations (3.2)–(3.5) for plasma virus concentration (in log₁₀ PFU ml⁻¹) over time post infection (blue) and experimental data on virus concentration (black). Parameters used are the mean for each species from the multi-level model. Data show the viraemia of the following species from [13]: (a–c) Monk parakeet, Canadian geese and common grackle, respectively. (Online version in colour.)

Figure 11.

(a–d) Posterior distribution of target cell limited model parameters for American crows. (e–h) Posterior distribution of target cell limited model parameters for Canadian geese. Parameters shown are V₀, inoculated virus density (PFU ml⁻¹); β, rate constant of infection (ml d⁻¹); p, infectious virus production rate (PFU d⁻¹); δ, death rate of productively infected cells (d⁻¹).

Figure 12.

Trace of samples from the Monte Carlo Markov Chain after burn-in and thinning (taking every 5th sample). (a–d) Trace of target cell limited model parameters for American crows. (e–h) Trace of target cell limited model parameters for Canadian geese. Parameters shown are V₀, inoculated virus density (PFU ml⁻¹); β, rate constant of infection (ml d⁻¹); p, infectious virus production rate (PFU d⁻¹); δ, death rate of productively infected cells (d⁻¹). (Online version in colour.)

Figure 13.

(a) Accuracy in viraemia prediction between multi-level model (blue) and aggregated model (red) for three different levels—individual, species and order. SSR—sum of squared residuals between model predicted viraemia and data. (b) A sample viraemia prediction from the multi-level (blue) and aggregated model (red).

Figure 14.

Posterior distribution of log₁₀ R₀ and burst size (log₁₀ p/δ) for the aggregated model (target cell limited model). (a,b) Aggregated model with all passerines (red), corvids (green) and non-passerines (blue). (c,d) Aggregated model with only passerines (red) and corvids (green). (e,f) Aggregated model with only corvids (green).