Persistence and reversal of plasmid-mediated antibiotic resistance

Abstract

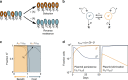
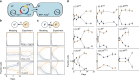
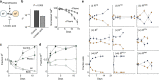
In the absence of antibiotic-mediated selection, sensitive bacteria are expected to displace their resistant counterparts if resistance genes are costly. However, many resistance genes persist for long periods in the absence of antibiotics. Horizontal gene transfer (primarily conjugation) could explain this persistence, but it has been suggested that very high conjugation rates would be required. Here, we show that common conjugal plasmids, even when costly, are indeed transferred at sufficiently high rates to be maintained in the absence of antibiotics in Escherichia coli. The notion is applicable to nine plasmids from six major incompatibility groups and mixed populations carrying multiple plasmids. These results suggest that reducing antibiotic use alone is likely insufficient for reversing resistance. Therefore, combining conjugation inhibition and promoting plasmid loss would be an effective strategy to limit conjugation-assisted persistence of antibiotic resistance.

Fig. 1

Conditions for plasmid persistence and elimination. a The concept of resistance reversal. A population initially consists of a mixture of sensitive (blue) and resistant (orange with plasmid) cells. In the presence of antibiotics (± indicates presence or absence of [A] antibiotic concentration), resistant cells are selected for. In the absence of antibiotics, as long as the plasmid imposes a fitness cost, then over a sufficiently long time the resistant cells will be presumably outcompeted, effectively reversing resistance. b Modeling plasmid dynamics in a single species (S). The plasmid-free population, S ⁰, acquires the plasmid through conjugation at a rate constant ${\eta }_{\mathrm{C}}$, becoming S ¹. S ¹ reverts to S ⁰ through plasmid loss at a rate constant κ. S ⁰ grows at a rate proportional to S ¹ (μ ₁ = μ, μ ₀ = αμ). The plasmid is costly when α > 1 and beneficial when α < 1. Both populations turnover at a constant dilution rate D. c Simulated fraction of S ¹ as a function of α and ${\eta }_{\mathrm{C}}$ after 5000 time units (~200 days). Fast conjugation can compensate for plasmid loss even if the plasmid carries a cost (α > 1). A greater ${\eta }_{\mathrm{C}}$ is required to maintain the plasmid population as α increases. d Criterion for plasmid persistence. If ${\eta }_{\mathrm{C}}$ > ${\eta }_{\mathrm{C}rit}=\alpha \left(\kappa +D\right)-D$, the plasmid will dominate (Eq. (1))

Fig. 2

Conjugation-assisted persistence of costly plasmids. For all modeling and experimental results, x-axis is days and y-axis is fraction of cells. a Engineered conjugation. The background strain, B, expresses BFP and Amp^R constitutively. B carries the helper plasmid F_HR (B⁰), which is non-self-transmissible, but can mobilize plasmids in trans. The mobile plasmid K carries the transfer origin (oriT), a kanamycin-resistant gene (Kan^R), and yfp under the control of strong constitutive promoter P_R . When B carries K, it is denoted B^K. K without transferability (i.e., without oriT) is denoted K⁻, and when carried by B, B^K−. b Long-term dynamics without conjugation. Blue represents plasmid-free and orange plasmid-carrying cells. Shaded lines indicate different initial conditions generated by a strong dilution experimentally (~80 cells/well, 16 wells), or randomly chosen from a uniform distribution (total initial density maintained at 1 × 10⁻⁶, 20 replicates). Bold lines are the average across all initial conditions of corresponding color. Modeling (left): i–iii is α = 1.02, 0.97, and 0.42, respectively, estimated from experimental measurements (Supplementary Fig. 1C). Experiment (right): i–iii is Kan = 0, 0.5, and 2 μg/mL. Quantification is performed using flow cytometry, where the orange lines are cells expressing both BFP and YFP (B^K−), and the blue line are cells expressing BFP only (B⁰). c Long-term dynamics with conjugation. Experiments were done identically to (B), with B^K instead of B^K−. Without antibiotics, the plasmid-carrying population dominated despite the plasmid cost, exhibiting conjugation-assisted persistence. All modeling parameters are identical except for ${\eta }_{\mathrm{C}}=0.025$ h⁻¹. d Nine conjugation plasmids carried by species R (except C with B⁰, which behaves similarly, Supplementary Fig. 3D) exhibit conjugation-assisted persistence. R⁰ was mixed in equal fraction with R^P (P for plasmid generality) and diluted 10,000× daily. CFU from four-to-six double-selection plates were divided by the total number of colonies averaged across four-to-six Cm plates for quantification. Experiments are repeated at least twice. Error bars represent the standard deviation of the four-to-six measurements. The plasmids used are (i) #168, (ii) #193, (iii) R388, (iv) C, (v) #41, (vi) RP4, (vii) K, (viii) PCU1, and (ix) R6K (see Supplementary Tables 1 and 3)

Fig. 3

Conjugation-assisted persistence with multiple species and/or plasmids. a–c x-axis is days and y-axis is fraction of cells. Bold and shaded lines represent average across, or individual, initial conditions, respectively. Color indicates blue for plasmid free (S ⁰), and orange or red for plasmid-carrying cells (S ¹) K or C, respectively. a Two-species, one-plasmid community. Left two panels: no conjugation; right two panels: with conjugation. S ⁰ = B⁰ + R⁰ and S ¹ = B^K + R^K. Modeling: From bottom (i) to top (iii) α ₁ = α = 1.02, 0.97, and 0.42, respectively, and α ₂ = 1.03, 1.02, and 0.9 (see Supplementary Eqs. (7)–(10), Supplementary Fig. 4A). Experiment from bottom (i) to top (iii): Kan = 0, 0.5, and 2 μg/mL, respectively. b Higher cost plasmid dynamics. Modeling (left column): From bottom (i) to top (iii) α = 1.13, 1.03, and 0.3, respectively (see Supplementary Eqs. (3)–(4), Supplementary Fig. 4B). Experiment (right column): From bottom (i) to top (iii): Cm = 0, 0.5, and 2 μg/mL. c One species, two-plasmid community. Each row represents a different combination of α, modulated with no antibiotic (i), Kan (ii–iii), or Cm (iv–v). The species can carry two (S ¹¹), one (S ¹⁰, S ⁰¹), or no plasmids (S ⁰⁰). Modeling (first and third columns): From bottom (i) to top (v) α ₃ = 1.3, 1.2, 0.42, 1.01, 0.35 (see Supplementary Eqs. (11)–(14), Supplementary Fig. 4B). Experiment: (second and fourth column such that S ¹ = B^K + B^CK or S ¹  = B^C + B^CK for K or C, respectively). B^C is mixed equally with B^K. d, e Three-species, three-plasmid community. Species (R, Y, and B) are uniquely fluorescent (expressing dTomato, YFP, or BFP, respectively) and plasmids (R6K, RP4, and R388, diamond, square, and circle markers, respectively) have distinct resistance markers (Strp^R, Kan^R, and Tm^R, respectively). Shading color corresponds to the respective population fraction (left y-axis), and markers indicate fraction of each plasmid (right y-axis). The initial experimental composition consists of R⁰, R^R6K, Y⁰, Y^R388, B⁰, and B^RP4. Modeling (left): Randomized initial conditions such that the total plasmid-free populations is maintained at 1 × 10⁻⁴ _, and plasmid population arbitrarily chosen between 1 × 10^–5 and 1 × 10⁶, consistent with data (Supplementary Table 2 for parameter estimates). Experiment (right): Error bars indicate averaging across four-to-six plate replicates, and repeated five times

Fig. 4

Reversing resistance due to conjugation-assisted persistence. a Combining inhibition of conjugation and promotion of plasmid loss to reverse resistance. This strategy is expected to increase ${\eta }_{\mathrm{C}rit}$ and decrease ${\eta }_{\mathrm{C}}$, potentially destabilizing the plasmid (Eq. (1)). b Evaluating conjugation inhibitor linoleic acid (Lin) and plasmid loss rate promoter phenothiazine (Pheno). Left: B^K and R⁰ were grown overnight with or without 3.25 mM Lin to quantify conjugation efficiency (see Methods). Right: B^K− was propagated daily in the presence of 50 μg/mL Kan, nothing, or 120 μM of Pheno. Kan was used as a control. Y-axis is the fraction of B^K− without antibiotic normalized by that treated with Kan quantified via flow cytometry. Pheno significantly increased the rate of plasmid loss by ~four-fold (see Supplementary Fig. 6B, right panel). c, d Inhibition of R^K and R⁴¹. R⁰ and R^K or R⁴¹ were mixed in equal fractions and diluted 10,000× daily for 11 days. Y-axis is fraction of plasmid-carrying cells and x-axis is days. Green shading indicates the treatments from dark to light: control, Pheno, Lin, and combined. Both plasmids were successfully reversed; when Lin was sufficient alone, Pheno had minimal effect (K). If Lin alone was insufficient, Lin with Pheno synergistically destabilized the plasmid. e Combination treatment with Lin and Pheno suppressed or reversed resistance. The same strains and protocol were used as in Fig. 2d, except media was supplemented with 3.25 mM Lin and 120 μM Pheno fresh daily (see Methods). The plasmids used are (i) #168, (ii) #193, (iii) R388, (iv) C, (v) #41, (vi) RP4, (vii) K, (viii) PCU1, and (ix) R6K (see Supplementary Tables 1 and 3). All CFU measurements were done in replicates of four-to-six plates, and repeated at least twice for reproducibility. All flow measurements were propagated with at least eight well replicates and repeated at least twice for reproducibility. Error bars represent the standard deviation of the plate or well replicates