A Sensitivity Analysis of an Inverted Pendulum Balance Control Model

Abstract

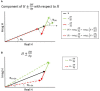
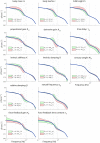
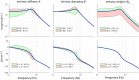
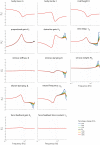
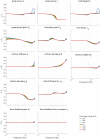
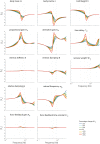
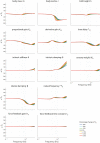
Balance control models are used to describe balance behavior in health and disease. We identified the unique contribution and relative importance of each parameter of a commonly used balance control model, the Independent Channel (IC) model, to identify which parameters are crucial to describe balance behavior. The balance behavior was expressed by transfer functions (TFs), representing the relationship between sensory perturbations and body sway as a function of frequency, in terms of amplitude (i.e., magnitude) and timing (i.e., phase). The model included an inverted pendulum controlled by a neuromuscular system, described by several parameters. Local sensitivity of each parameter was determined for both the magnitude and phase using partial derivatives. Both the intrinsic stiffness and proportional gain shape the magnitude at low frequencies (0.1-1 Hz). The derivative gain shapes the peak and slope of the magnitude between 0.5 and 0.9 Hz. The sensory weight influences the overall magnitude, and does not have any effect on the phase. The effect of the time delay becomes apparent in the phase above 0.6 Hz. The force feedback parameters and intrinsic stiffness have a small effect compared with the other parameters. All parameters shape the TF magnitude and phase and therefore play a role in the balance behavior. The sensory weight, time delay, derivative gain, and the proportional gain have a unique effect on the TFs, while the force feedback parameters and intrinsic stiffness contribute less. More insight in the unique contribution and relative importance of all parameters shows which parameters are crucial and critical to identify underlying differences in balance behavior between different patient groups.

Keywords: balance control model; frequency domain; human balance control; parameters; sensitivity analysis.

Figure 1

Inverted pendulum balance control model. The human body is represented by an inverted pendulum (IP) with corresponding body dynamics (BD), which is controlled by the neuromuscular system consisting of the neural controller (NC) incorporating a PD controller with neural signal transport delay and muscle activation dynamics, and the intrinsic muscle properties (P). The NC receives a weighted combination of body orientation information from the sensory systems (W) (i.e., graviceptive, visual, and proprioceptive system) and force feedback information (F) from the force sensors. The total corrective ankle torque consists of the output of the NC processed through muscle activation dynamics plus the torque arising from the intrinsic muscle properties (P). The proprioceptive and visual sensory systems can be perturbed by support surface (SS) and visual surround (VS) rotations, respectively.

Figure 2

Representation of adding (green) or subtracting (red) the (normalized or scaled) partial derivatives from the transfer function H at one frequency resulting in a change in magnitude (A) and change in phase (B).

Figure 3

Sensitivity of each parameter of the model's transfer function from support surface rotation to body sway (H_SS) on the TF magnitude represented by adding or subtracting the partial derivatives from the TF magnitude; green indicates the effect of a parameter increase and red a parameter decrease. The partial derivatives are multiplied by a scaling factor such that the relative maximum change of the magnitude is 0.7.

Figure 4

Sensitivity of each parameter of the model's transfer function from support surface rotation to body sway (H_SS) on the TF phase represented by adding or subtracting the partial derivatives from the TF phase; green indicates the effect of a parameter increase and red a parameter decrease. The partial derivatives are multiplied by a scaling factor such that the relative maximum change of the magnitude is 0.7.

Figure 5

Sensitivity of the sensory weight (W_V), intrinsic stiffness (K), and intrinsic damping (B) of the model's transfer function from visual surround rotation to body sway (H_VS) on the magnitude and phase represented by adding or subtracting the partial derivatives from the TF magnitude or phase; green indicates the effect of a parameter increase and red a parameter decrease. The partial derivatives are multiplied by a scaling factor such that the relative maximum change of the magnitude is 0.7.

Figure 6

Change in the normalized sensitivity of each parameter of the model's transfer function from support surface rotation to body sway (H_SS) on the TF magnitude with systematically changing the sensory weight.

Figure 7

Change in the normalized sensitivity of each parameter of the model's transfer function from support surface rotation to body sway (H_SS) on the TF phase with systematically changing the sensory weight.

Figure 8

Change in the normalized sensitivity of each parameter of the model's transfer function from support surface rotation to body sway (H_SS) on the TF magnitude with systematically changing the time delay.

Figure 9

Change in the normalized sensitivity of each parameter of the model's transfer function from support surface rotation to body sway (H_SS) on the TF phase with systematically changing the time delay.