Mortality Trajectories at Exceptionally High Ages: A Study of Supercentenarians

Abstract

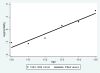
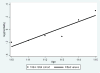
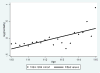
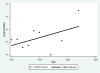
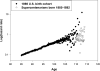
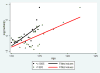
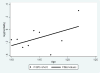
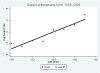
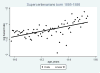
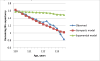
The growing number of persons surviving to age 100 years and beyond raises questions about the shape of mortality trajectories at exceptionally high ages, and this problem may become significant for actuaries in the near future. However, such studies are scarce because of the difficulties in obtaining reliable age estimates at exceptionally high ages. The current view about mortality beyond age 110 years suggests that death rates do not grow with age and are virtually flat. The same assumption is made in the new actuarial VBT tables. In this paper, we test the hypothesis that the mortality of supercentenarians (persons living 110+ years) is constant and does not grow with age, and we analyze mortality trajectories at these exceptionally high ages. Death records of supercentenarians were taken from the International Database on Longevity (IDL). All ages of supercentenarians in the database were subjected to careful validation. We used IDL records for persons belonging to extinct birth cohorts (born before 1895) since the last deaths in IDL were observed in 2007. We also compared our results based on IDL data with a more contemporary database maintained by the Gerontology Research Group (GRG). First we attempted to replicate findings by Gampe (2010), who analyzed IDL data and came to the conclusion that "human mortality after age 110 is flat." We split IDL data into two groups: cohorts born before 1885 and cohorts born in 1885 and later. Hazard rate estimates were conducted using the standard procedure available in Stata software. We found that mortality in both groups grows with age, although in older cohorts, growth was slower compared with more recent cohorts and not statistically significant. Mortality analysis of more numerous 1884-1894 birth cohort with the Akaike goodness-of-fit criterion showed better fit for the Gompertz model than for the exponential model (flat mortality). Mortality analyses with GRG data produced similar results. The remaining life expectancy for the 1884-1894 birth cohort demonstrates rapid decline with age. This decline is similar to the computer-simulated trajectory expected for the Gompertz model, rather than the extremely slow decline in the case of the exponential model. These results demonstrate that hazard rates after age 110 years do not stay constant and suggest that mortality deceleration at older ages is not a universal phenomenon. These findings may represent a challenge to the existing theories of aging and longevity, which predict constant mortality in the late stages of life. One possibility for reconciliation of the observed phenomenon and the existing theoretical consideration is a possibility of mortality deceleration and mortality plateau at very high yet unobservable ages.

Fig. 1. Age-Specific Hazard Rates for Supercentenarians Born in 1884–1894, Fitted by the Gompertz Model

Note: Yearly age intervals. The data fits well with the straight line in semi-log scale, as predicted by the Gompertz model, with no sign of mortality deceleration at extreme old ages.

Fig. 2. Hazard Rates as a Function of Age for Supercentenarians Born in the United States, 1884–1894

Note: Yearly age intervals. The data fits well with the straight line in semi-log scale, as predicted by the Gompertz model.

Fig. 3. Hazard Rates as a Function of Age for Supercentenarians Born in 1884–1894 with High-Quality Age Validation (Group A)

Note: Yearly age intervals. The data fits well with the straight line in semi-log scale, as predicted by the Gompertz model.

Fig. 4. Hazard Rates, Measured at Quarterly Intervals, as a Function of Age for Supercentenarians Born in 1884–1894

Note: The data fits well with the straight line in semi-log scale, as predicted by the Gompertz model.

Fig. 5. Age-Specific Hazard Rates for Supercentenarians Born Before 1885, Fitted by the Gompertz Model

Note: The hazard rate grows with age, although data fit is not as good as for more recent birth cohorts.

Fig. 6. Mortality of Supercentenarians Compared With Mortality of the 1898 U.S. Birth Cohort

Fig. 7. Age-Specific Hazard Rates for Supercentenarians Born Before 1885 and in 1885 and Later, Fitted by the Gompertz Model

Fig. 8. Age-Specific Hazard Rates for Female and Male Supercentenarians Born in 1884– 1894

Fig. 9. Hazard Rate, Measured at Yearly Age Intervals, as a Function of Age for Supercentenarians From the GRG Database Born in 1885–1898

Note: The data fits well with the straight line in semi-log scale, as predicted by the Gompertz model.

Fig. 10. Hazard Rate, Measured at Monthly Age Intervals, as a Function of Age for Supercentenarians From the GRG Database Born in 1885–1898

Note: The data fits well with the straight line in semi-log scale, as predicted by the Gompertz model.

Fig. 11. Changes in Life Expectancy With Age After 110 Years: Remaining Life Expectancy of Supercentenarians Born in 1884–1894 Compared with Simulations Using the Exponential and Gompertz Models

Note: The observed life expectancy declines with age, and its trajectory is closer to the Gompertz model, which does not agree with the assumption about a flat hazard rate (exponential model of survival).

Fig. 12. Hazard Rate Change Over Age for Older (Born Before 1885) and Younger (Born 1885 or After) Birth Cohorts of Supercentenarians

Note: Quarterly estimates. The tendency of mortality growth with age (which is visible on a semi-log scale) is lost when data are analyzed using a plain scale.