Characteristic impedance: frequency or time domain approach?
- PMID: 29176040
- PMCID: PMC5828940
- DOI: 10.1088/1361-6579/aa9d60
Characteristic impedance: frequency or time domain approach?
Abstract
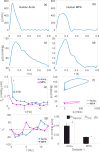
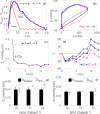
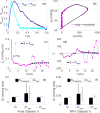
Objective: Characteristic impedance (Zc) is an important component in the theory of hemodynamics. It is a commonly used metric of proximal arterial stiffness and pulse wave velocity. Calculated using simultaneously measured dynamic pressure and flow data, estimates of characteristic impedance can be obtained using methods based on frequency or time domain analysis. Applications of these methods under different physiological and pathological conditions in species with different body sizes and heart rates show that the two approaches do not always agree. In this study, we have investigated the discrepancies between frequency and time domain estimates accounting for uncertainties associated with experimental processes and physiological conditions.
Approach: We have used published data measured in different species including humans, dogs, and mice to investigate: (a) the effects of time delay and signal noise in the pressure-flow data, (b) uncertainties about the blood flow conditions, (c) periodicity of the cardiac cycle versus the breathing cycle, on the frequency and time domain estimates of Zc, and (d) if discrepancies observed under different hemodynamic conditions can be eliminated. Main results and Significance: We have shown that the frequency and time domain estimates are not equally sensitive to certain characteristics of hemodynamic signals including phase lag between pressure and flow, signal to noise ratio and the end of systole retrograde flow. The discrepancies between two types of estimates are inherent due to their intrinsically different mathematical expressions and therefore it is impossible to define a criterion to resolve such discrepancies. Considering the interpretation and role of Zc as an important hemodynamic parameter, we suggest that the frequency and time domain estimates should be further assessed as two different hemodynamic parameters in a future study.
Figures
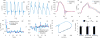




References
-
- Abel FL. Fourier analysis of left ventricular performance. Circ Res. 1971;28:119–35. - PubMed
-
- Bak Z, Sjoberg F, Rousseau A, Steinvall I, Janerot-Sjoberg B. Human cardiovascular dose-response to supplemental oxygen. Acta Physiologica. 2007;191:15–24. - PubMed
-
- Bergel DH, Milnor WH. Pulmonary vascular impedance in dog. Circ Res. 1965;16:401–15. - PubMed
-
- Bollache E, Kachenoura N, Bargiotas I, Giron A, Cesare AD, Bensalah M, Lucor D, Redheuil A, Mousseaux E. How to estimate aortic characteristic impedance from magnetic resonance and applanation tonometry data? J Hypertension. 2015;33:575–83. - PubMed
-
- Borlotti A, Li Y, Parker KH, Khir AW. Experimental evaluation of local wave speed in the presence of reflected waves. J Biomech. 2014;47:87–95. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
