Mechanical control of growth: ideas, facts and challenges
- PMID: 29183937
- PMCID: PMC5769630
- DOI: 10.1242/dev.151902
Mechanical control of growth: ideas, facts and challenges
Abstract
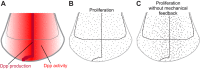
In his classic book On Growth and Form, D'Arcy Thompson discussed the necessity of a physical and mathematical approach to understanding the relationship between growth and form. The past century has seen extraordinary advances in our understanding of biological components and processes contributing to organismal morphogenesis, but the mathematical and physical principles involved have not received comparable attention. The most obvious entry of physics into morphogenesis is via tissue mechanics. In this Review, we discuss the fundamental role of mechanical interactions between cells induced by growth in shaping a tissue. Non-uniform growth can lead to accumulation of mechanical stress, which in the context of two-dimensional sheets of tissue can specify the shape it assumes in three dimensions. A special class of growth patterns - conformal growth - does not lead to the accumulation of stress and can generate a rich variety of planar tissue shapes. Conversely, mechanical stress can provide a regulatory feedback signal into the growth control circuit. Both theory and experiment support a key role for mechanical interactions in shaping tissues and, via mechanical feedback, controlling epithelial growth.
Keywords: Growth; Hippo; Mechanics; Stress.
© 2017. Published by The Company of Biologists Ltd.
Conflict of interest statement
Competing interestsThe authors declare no competing or financial interests.
Figures
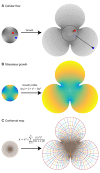
 , where z=x+iy is a complex number constructed from spatial coordinates (x, y) generated by the growth profile γ specified above (see
, where z=x+iy is a complex number constructed from spatial coordinates (x, y) generated by the growth profile γ specified above (see 

References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

