Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator
- PMID: 29189781
- PMCID: PMC6506159
- DOI: 10.1038/nature24654
Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator
Abstract
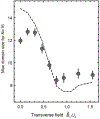
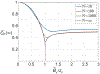
A quantum simulator is a type of quantum computer that controls the interactions between quantum bits (or qubits) in a way that can be mapped to certain quantum many-body problems. As it becomes possible to exert more control over larger numbers of qubits, such simulators will be able to tackle a wider range of problems, such as materials design and molecular modelling, with the ultimate limit being a universal quantum computer that can solve general classes of hard problems. Here we use a quantum simulator composed of up to 53 qubits to study non-equilibrium dynamics in the transverse-field Ising model with long-range interactions. We observe a dynamical phase transition after a sudden change of the Hamiltonian, in a regime in which conventional statistical mechanics does not apply. The qubits are represented by the spins of trapped ions, which can be prepared in various initial pure states. We apply a global long-range Ising interaction with controllable strength and range, and measure each individual qubit with an efficiency of nearly 99 per cent. Such high efficiency means that arbitrary many-body correlations between qubits can be measured in a single shot, enabling the dynamical phase transition to be probed directly and revealing computationally intractable features that rely on the long-range interactions and high connectivity between qubits.
Conflict of interest statement
The authors declare competing financial interests: C. M. is a founding scientist of ionQ, Inc.
Figures
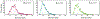
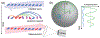
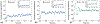
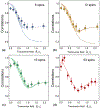

Comment in
-
Large quantum systems tamed.Nature. 2017 Nov 30;551(7682):569-571. doi: 10.1038/d41586-017-07438-8. Nature. 2017. PMID: 29189795 No abstract available.
References
-
- Feynman RP Simulating physics with computers. Int. J. Theor. Phys 21, 467–488 (1982).
-
- Trabesinger A et al. Nature physics insight–quantum simulation. Nature Phys 8, 263–299 (2012).
-
- Nielsen MA & Chuang IL Quantum Computation and Quantum Information (Cambridge University Press, New York, NY, USA, 2011), 10th anniv. edn.
-
- Hinrichsen H Non-equilibrium phase transitions. Physica A 369, 1–28 (2006).
-
- Richerme P et al. Non-local propagation of correlations in quantum systems with long-range interactions. Nature 511, 198 (2014). - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

