Robust Low-Dose CT Sinogram Preprocessing via Exploiting Noise-Generating Mechanism
- PMID: 29192885
- PMCID: PMC5718215
- DOI: 10.1109/TMI.2017.2767290
Robust Low-Dose CT Sinogram Preprocessing via Exploiting Noise-Generating Mechanism
Abstract
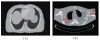
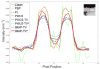
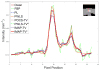
Computed tomography (CT) image recovery from low-mAs acquisitions without adequate treatment is always severely degraded due to a number of physical factors. In this paper, we formulate the low-dose CT sinogram preprocessing as a standard maximum a posteriori (MAP) estimation, which takes full consideration of the statistical properties of the two intrinsic noise sources in low-dose CT, i.e., the X-ray photon statistics and the electronic noise background. In addition, instead of using a general image prior as found in the traditional sinogram recovery models, we design a new prior formulation to more rationally encode the piecewise-linear configurations underlying a sinogram than previously used ones, like the TV prior term. As compared with the previous methods, especially the MAP-based ones, both the likelihood/loss and prior/regularization terms in the proposed model are ameliorated in a more accurate manner and better comply with the statistical essence of the generation mechanism of a practical sinogram. We further construct an efficient alternating direction method of multipliers algorithm to solve the proposed MAP framework. Experiments on simulated and real low-dose CT data demonstrate the superiority of the proposed method according to both visual inspection and comprehensive quantitative performance evaluation.
Figures









Similar articles
-
Realistic simulation of reduced-dose CT with noise modeling and sinogram synthesis using DICOM CT images.Med Phys. 2014 Jan;41(1):011901. doi: 10.1118/1.4830431. Med Phys. 2014. PMID: 24387509
-
Noise-Generating and Imaging Mechanism Inspired Implicit Regularization Learning Network for Low Dose CT Reconstrution.IEEE Trans Med Imaging. 2024 May;43(5):1677-1689. doi: 10.1109/TMI.2023.3347258. Epub 2024 May 2. IEEE Trans Med Imaging. 2024. PMID: 38145543
-
Ultra-low dose CT attenuation correction for PET/CT: analysis of sparse view data acquisition and reconstruction algorithms.Phys Med Biol. 2015 Oct 7;60(19):7437-60. doi: 10.1088/0031-9155/60/19/7437. Epub 2015 Sep 9. Phys Med Biol. 2015. PMID: 26352168 Free PMC article.
-
Dual energy CT for attenuation correction with PET/CT.Med Phys. 2014 Jan;41(1):012501. doi: 10.1118/1.4828838. Med Phys. 2014. PMID: 24387525 Free PMC article.
-
Regularization strategies in statistical image reconstruction of low-dose x-ray CT: A review.Med Phys. 2018 Oct;45(10):e886-e907. doi: 10.1002/mp.13123. Epub 2018 Sep 10. Med Phys. 2018. PMID: 30098050 Free PMC article. Review.
Cited by
-
Recent Progress Toward Imaging Application of Multifunction Sonosensitizers in Sonodynamic Therapy.Int J Nanomedicine. 2022 Aug 6;17:3511-3529. doi: 10.2147/IJN.S370767. eCollection 2022. Int J Nanomedicine. 2022. PMID: 35966148 Free PMC article. Review.
-
Chest Computed Tomography Images in Neonatal Bronchial Pneumonia under the Adaptive Statistical Iterative Reconstruction Algorithm.J Healthc Eng. 2021 Oct 27;2021:6183946. doi: 10.1155/2021/6183946. eCollection 2021. J Healthc Eng. 2021. PMID: 34745505 Free PMC article.
-
[CT image quality assessment based on prior information of pre-restored images].Nan Fang Yi Ke Da Xue Xue Bao. 2021 Feb 25;41(2):230-237. doi: 10.12122/j.issn.1673-4254.2021.02.10. Nan Fang Yi Ke Da Xue Xue Bao. 2021. PMID: 33624596 Free PMC article. Chinese.
-
Bilateral Weighted Relative Total Variation for Low-Dose CT Reconstruction.J Digit Imaging. 2023 Apr;36(2):458-467. doi: 10.1007/s10278-022-00720-w. Epub 2022 Nov 28. J Digit Imaging. 2023. PMID: 36443529 Free PMC article.
-
Self-adaption and texture generation: A hybrid loss function for low-dose CT denoising.J Appl Clin Med Phys. 2023 Sep;24(9):e14113. doi: 10.1002/acm2.14113. Epub 2023 Aug 11. J Appl Clin Med Phys. 2023. PMID: 37571834 Free PMC article.
References
-
- Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. Siam Journal on Imaging Sciences. 2009;2(1):183–202.
-
- Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations & Trends in Machine Learning. 2011;3(1):1–122.
-
- Boyd VLS. Convex optimization. Cambridge university press; 2004.
-
- Chambolle A, Lions PL. Image recovery via total variation minimization and related problems. Numerische Mathematik. 1997;76(2):167–188.
-
- Chen C, He B, Ye Y, Yuan X. The direct extension of admm for multi-block convex minimization problems is not necessarily convergent. Mathematical Programming. 2016;155(1):57–79.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

