Robust Low-Dose CT Sinogram Preprocessing via Exploiting Noise-Generating Mechanism

Abstract

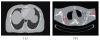
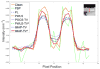
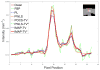
Computed tomography (CT) image recovery from low-mAs acquisitions without adequate treatment is always severely degraded due to a number of physical factors. In this paper, we formulate the low-dose CT sinogram preprocessing as a standard maximum a posteriori (MAP) estimation, which takes full consideration of the statistical properties of the two intrinsic noise sources in low-dose CT, i.e., the X-ray photon statistics and the electronic noise background. In addition, instead of using a general image prior as found in the traditional sinogram recovery models, we design a new prior formulation to more rationally encode the piecewise-linear configurations underlying a sinogram than previously used ones, like the TV prior term. As compared with the previous methods, especially the MAP-based ones, both the likelihood/loss and prior/regularization terms in the proposed model are ameliorated in a more accurate manner and better comply with the statistical essence of the generation mechanism of a practical sinogram. We further construct an efficient alternating direction method of multipliers algorithm to solve the proposed MAP framework. Experiments on simulated and real low-dose CT data demonstrate the superiority of the proposed method according to both visual inspection and comprehensive quantitative performance evaluation.

Fig. 1

(a) An example of noise-free CT image. (b) The amplified illustration of the red box in (a). (c) The FBP reconstruction result with only simulated quanta fluctuation added to projection data. (d) The FBP reconstruction result with only simulated electronic noise added to projection data. (e) The FBP reconstruction result with both simulated quanta fluctuation and simulated electronic noise added to projection data.

Fig. 2

(a) The manifold of an example sinogram data with axis along detector elements and projection views. The upper right is the illustration of the example sinogram. The upper left is the amplified area at a 2.5 times larger scale for easy observation of details; (b) and (c) are the absolute of the first and second order vertical derivatives calculated on the example sinogram, respectively, where the deeper the color is, the larger the value is. It can be observed from (a) that it is better to describe the sinogram as piecewise linear rather than piecewise constant (as what TV encourages). From (b) and (c), one can see that the second order derivative of a sinogram is evidently more sparse the first order one.

Fig. 3

(a) illustration of the 1^st frame of the noise-free digital myocardial perfusion phantom; (b) The noise-free image anthropomorphic torso phantom.

Fig. 4

(a) The noise-free digital XCAT image; (b)–(h) The images reconstructed by the FBP PL, PWLS, POCS-TV, PWLS-TV², IMAP-TV and IMAP-TV² methods at 20 mAs, respectively. The demarcated area in each image is amplified at a 3 time larger scale for easy observation.

Fig. 5

The vertical profiles of the noise-free image and recovery results of the 7 competing methods of digital XCAT images at 20 mAs. The vertical profiles is located at the pixel positions x = 245 and y from 155 to 180. as shown in Fig. 3(a).

Fig. 6

(a) The noise-free image of the anthropomorphic torso phantom study; (b)–(h) The images reconstructed by FBP. PL, PWLS, POCS-TV, PWLS-TV², IMAP-TV and IMAP-TV² at 17 mAs, respectively. The demarcated area in each image is amplified at a 3 time larger scale for easy observation of details.

Fig. 7

The vertical profiles of the noise-free image and recovery result of the 7 methods of digital anthropomorphic torso phantom at 17 mAs. The vertical profiles is located at the pixel positions x = 240 and y from 160 to 195. as shown in Fig. 3(b).

Fig. 8

The NVF images at the position shown as ROI 3 in Fig. 3(b), (a) noise-free image, (b)–(h) the results reconstructed by FBP, PL, PWLS, POCS-TV, PWLS-TV², IMAP-TV and IMAP-TV².

Fig. 9

(a)–(f) Residuals of the result reconstructed by PL, PWLS, POCS-TV, PWLS-TV², IMAP-TV, IMAP-TV² at 17 mAs, respectively.

Fig. 10

Comparison of ROI reconstructed by the 6 competing methods.

Fig. 11

(a) The high-dose image of the 11^th frame of preclinical porcine data; (b)–(h) The images reconstructed by the FBP, PL, PWLS, POCS-TV, PWLS-TV², IMAP-TV and IMAP-TV² methods at 20 mAs, respectively. The demarcated area in each image is amplified at a 3 time larger scale for easy observation.

Fig. 12

(a) The MBF maps from high-dose images; (b)–(h) The MBF maps from simulated low-dose images reconstructed by FBP, PL, PWLS, POCS-TV, PWLS-TV². IMAP-TV and IMAP-TV² methods, respectively. The demarcated area in each image is amplified at a 3 time larger scale for easy observation.