A model of individualized canonical microcircuits supporting cognitive operations
- PMID: 29200435
- PMCID: PMC5714354
- DOI: 10.1371/journal.pone.0188003
A model of individualized canonical microcircuits supporting cognitive operations
Abstract
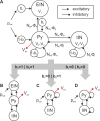
Major cognitive functions such as language, memory, and decision-making are thought to rely on distributed networks of a large number of basic elements, called canonical microcircuits. In this theoretical study we propose a novel canonical microcircuit model and find that it supports two basic computational operations: a gating mechanism and working memory. By means of bifurcation analysis we systematically investigate the dynamical behavior of the canonical microcircuit with respect to parameters that govern the local network balance, that is, the relationship between excitation and inhibition, and key intrinsic feedback architectures of canonical microcircuits. We relate the local behavior of the canonical microcircuit to cognitive processing and demonstrate how a network of interacting canonical microcircuits enables the establishment of spatiotemporal sequences in the context of syntax parsing during sentence comprehension. This study provides a framework for using individualized canonical microcircuits for the construction of biologically realistic networks supporting cognitive operations.
Conflict of interest statement
Figures









Similar articles
-
Emergence of cognitive priming and structure building from the hierarchical interaction of canonical microcircuit models.Biol Cybern. 2019 Jun;113(3):273-291. doi: 10.1007/s00422-019-00792-y. Epub 2019 Feb 14. Biol Cybern. 2019. PMID: 30767085 Free PMC article.
-
Working Memory and Decision-Making in a Frontoparietal Circuit Model.J Neurosci. 2017 Dec 13;37(50):12167-12186. doi: 10.1523/JNEUROSCI.0343-17.2017. Epub 2017 Nov 7. J Neurosci. 2017. PMID: 29114071 Free PMC article.
-
Toward a prefrontal microcircuit model for cognitive deficits in schizophrenia.Pharmacopsychiatry. 2006 Feb;39 Suppl 1:S80-7. doi: 10.1055/s-2006-931501. Pharmacopsychiatry. 2006. PMID: 16508903
-
Memory mechanisms supporting syntactic comprehension.Psychon Bull Rev. 2013 Apr;20(2):243-68. doi: 10.3758/s13423-012-0369-9. Psychon Bull Rev. 2013. PMID: 23319178 Free PMC article. Review.
-
Early Visual Cortex as a Multiscale Cognitive Blackboard.Annu Rev Vis Sci. 2016 Oct 14;2:131-151. doi: 10.1146/annurev-vision-111815-114443. Epub 2016 Jul 18. Annu Rev Vis Sci. 2016. PMID: 28532363 Review.
Cited by
-
Emergence of cognitive priming and structure building from the hierarchical interaction of canonical microcircuit models.Biol Cybern. 2019 Jun;113(3):273-291. doi: 10.1007/s00422-019-00792-y. Epub 2019 Feb 14. Biol Cybern. 2019. PMID: 30767085 Free PMC article.
-
Rate and oscillatory switching dynamics of a multilayer visual microcircuit model.Elife. 2022 Aug 22;11:e77594. doi: 10.7554/eLife.77594. Elife. 2022. PMID: 35994330 Free PMC article.
-
Attention modulates topology and dynamics of auditory sensory gating.Hum Brain Mapp. 2019 Jul;40(10):2981-2994. doi: 10.1002/hbm.24573. Epub 2019 Mar 18. Hum Brain Mapp. 2019. PMID: 30882981 Free PMC article.
References
-
- Friederici AD, Singer W. Grounding language processing on basic neurophysiological principles. Trends in cognitive sciences. 2015;19(6):329–38. Epub 2015/04/22. doi: 10.1016/j.tics.2015.03.012 . - DOI - PubMed
-
- Miller KD. Canonical computations of cerebral cortex. Current opinion in neurobiology. 2016;37:75–84. Epub 2016/02/13. doi: 10.1016/j.conb.2016.01.008 ; PubMed Central PMCID: PMCPmc4944655. - DOI - PMC - PubMed
-
- Treves A. Frontal latching networks: a possible neural basis for infinite recursion. Cognitive neuropsychology. 2005;22(3):276–91. Epub 2005/01/01. doi: 10.1080/02643290442000329 . - DOI - PubMed
-
- Mountcastle VB. Modality and topographic properties of single neurons of cat's somatic sensory cortex. Journal of neurophysiology. 1957;20(4):408–34. Epub 1957/07/01. . - PubMed
-
- Lubke J, Feldmeyer D. Excitatory signal flow and connectivity in a cortical column: focus on barrel cortex. Brain structure & function. 2007;212(1):3–17. Epub 2007/08/25. doi: 10.1007/s00429-007-0144-2 . - DOI - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

