Effect of parameter selection on entropy calculation for long walking trials

Abstract

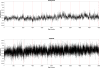
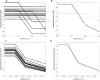
It is sometimes difficult to obtain uninterrupted data sets that are long enough to perform nonlinear analysis, especially in pathological populations. It is currently unclear as to how many data points are needed for reliable entropy analysis. The aims of this study were to determine the effect of changing parameter values of m, r, and N on entropy calculations for long gait data sets using two different modes of walking (i.e., overground versus treadmill). Fourteen young adults walked overground and on a treadmill at their preferred walking speed for one-hour while step time was collected via heel switches. Approximate (ApEn) and sample entropy (SampEn) were calculated using multiple parameter combinations of m, N, and r. Further, r was tested under two cases r*standard deviation and r constant. ApEn differed depending on the combination of r, m, and N. ApEn demonstrated relative consistency except when m=2 and the smallest r values used (rSD=0.015*SD, 0.20*SD; rConstant=0 and 0.003). For SampEn, as r increased, SampEn decreased. When r was constant, SampEn demonstrated excellent relative consistency for all combinations of r, m, and N. When r constant was used, overground walking was more regular than treadmill. However, treadmill walking was found to be more regular when using rSD for both ApEn and SampEn. For greatest relative consistency of step time data, it was best to use a constant r value and SampEn. When using entropy, several r values must be examined and reported to ensure that results are not an artifact of parameter choice.

Keywords: Complexity; Gait; Locomotion; Predictability; Regularity; Treadmill.

Figure 1

Data from a representative subject for overground (top) and treadmill (bottom) step times.

Figure 2

ApEn (diamond) and SampEn (square) as a function of step time data length for r=0.15 (A), 0.20 (B), 0.25 (C), and 0.30 (D) multiplied by the standard deviation for overground (gray) and treadmill (black) walking when m=2.

Figure 3

ApEn (diamond) and SampEn (square) as a function of step time data length for r=0.15 (A), 0.20 (B), 0.25 (C), and 0.30 (D) multiplied by the standard deviation for overground (gray) and treadmill (black) walking when m=3.

Figure 4

SampEn as a function of tolerance are plotted for all overground (gray) and treadmill (black) step time time series (m=2, N=5000). The top row represents rSD entropy values where the bottom row represents rConstant values. Treadmill and overground trials for each subject are plotted (A & C) as well as the group average (C & D). When r is multiplied by the SD (A), the tolerance for comparisons is too small for like-matches to be found within each time series. When the tolerance reaches a critical level, the number of matches increases allowing the entropy value to drop in the treadmill trials. This causes a “stair step” decrease in entropy across r values in some trials. Enough of the subjects’ time series reached this critical level when r increased from 0.20 to 0.25*standard deviation (B) and overground entropy then became greater than treadmill entropy. When r is held constant (C & D) and not multiplied by the standard deviation of the time series, the SampEn value decreases with every increase in r.

Figure 5

ApEn (diamond) and SampEn (square) as a function of step time data length for r=0.0 (A), 0.003 (B), 0.007 (C), and 0.013 (D) for overground (gray) and treadmill (black) walking when m=2.

Figure 6

ApEn (diamond) and SampEn (square) as a function of step time data length for r=0.0 (A), 0.003 (B), 0.007 (C), and 0.013 (D) for overground (gray) and treadmill (black) walking when m=3.