Origami lattices with free-form surface ornaments
- PMID: 29209661
- PMCID: PMC5710187
- DOI: 10.1126/sciadv.aao1595
Origami lattices with free-form surface ornaments
Abstract
Lattice structures are used in the design of metamaterials to achieve unusual physical, mechanical, or biological properties. The properties of such metamaterials result from the topology of the lattice structures, which are usually three-dimensionally (3D) printed. To incorporate advanced functionalities into metamaterials, the surface of the lattice structures may need to be ornamented with functionality-inducing features, such as nanopatterns or electronic devices. Given our limited access to the internal surfaces of lattice structures, free-form ornamentation is currently impossible. We present lattice structures that are folded from initially flat states and show that they could bear arbitrarily complex surface ornaments at different scales. We identify three categories of space-filling polyhedra as the basic unit cells of the cellular structures and, for each of those, propose a folding pattern. We also demonstrate "sequential self-folding" of flat constructs to 3D lattices. Furthermore, we folded auxetic mechanical metamaterials from flat sheets and measured the deformation-driven change in their negative Poisson's ratio. Finally, we show how free-form 3D ornaments could be applied on the surface of flat sheets with nanometer resolution. Together, these folding patterns and experimental techniques present a unique platform for the fabrication of metamaterials with unprecedented combination of physical properties and surface-driven functionalities.
Figures


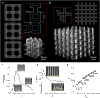

References
-
- Valentine J., Zhang S., Zentgraf T., Ulin-Avila E., Genov D. A., Bartal G., Zhang X., Three-dimensional optical metamaterial with a negative refractive index. Nature 455, 376–379 (2008). - PubMed
-
- Shalaev V. M., Optical negative-index metamaterials. Nat. Photonics 1, 41–48 (2007).
-
- Pryce I. M., Aydin K., Kelaita Y. A., Briggs R. M., Atwater H. A., Highly strained compliant optical metamaterials with large frequency tunability. Nano Lett. 10, 4222–4227 (2010). - PubMed
-
- Schurig D., Mock J. J., Justice B. J., Cummer S. A., Pendry J. B., Starr A. F., Smith D. R., Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006). - PubMed
-
- Zhang S., Xia C., Fang N., Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 106, 024301 (2011). - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

