Graph-facilitated resonant mode counting in stochastic interaction networks
- PMID: 29212754
- PMCID: PMC5746565
- DOI: 10.1098/rsif.2017.0447
Graph-facilitated resonant mode counting in stochastic interaction networks
Abstract
Oscillations in dynamical systems are widely reported in multiple branches of applied mathematics. Critically, even a non-oscillatory deterministic system can produce cyclic trajectories when it is in a low copy number, stochastic regime. Common methods of finding parameter ranges for stochastically driven resonances, such as direct calculation, are cumbersome for any but the smallest networks. In this paper, we provide a systematic framework to efficiently determine the number of resonant modes and parameter ranges for stochastic oscillations relying on real root counting algorithms and graph theoretic methods. We argue that stochastic resonance is a network property by showing that resonant modes only depend on the squared Jacobian matrix J2, unlike deterministic oscillations which are determined by J By using graph theoretic tools, analysis of stochastic behaviour for larger interaction networks is simplified and stochastic dynamical systems with multiple resonant modes can be identified easily.
Keywords: chemical reaction networks; graph theoretic methods; quasi-cycles; resonant modes; sturm chains.
© 2017 The Authors.
Conflict of interest statement
We declare we have no competing interests.
Figures
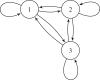

 ,
, 
 and
and 
 .
.




References
-
- Wang W, Chen L. 1997. A predator-prey system with stage-structure for predator. Comput. Math. Appl. 33, 83–91. (10.1016/S0898-1221(97)00056-4) - DOI
-
- Lotka AJ. 1925. Elements of physical biology. Baltimore, MD: Williams & Wilkins Co.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
