Robust mixture modeling reveals category-free selectivity in reward region neuronal ensembles

Abstract

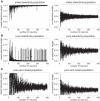
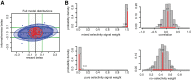
Classification of neurons into clusters based on their response properties is an important tool for gaining insight into neural computations. However, it remains unclear to what extent neurons fall naturally into discrete functional categories. We developed a Bayesian method that models the tuning properties of neural populations as a mixture of multiple types of task-relevant response patterns. We applied this method to data from several cortical and striatal regions in economic choice tasks. In all cases, neurons fell into only two clusters: one multiple-selectivity cluster containing all cells driven by task variables of interest and another of no selectivity for those variables. The single cluster of task-sensitive cells argues against robust categorical tuning in these areas. The no-selectivity cluster was unanticipated and raises important questions about what distinguishes these neurons and what role they play. Moreover, the ability to formally identify these nonselective cells allows for more accurate measurement of ensemble effects by excluding or appropriately down-weighting them in analysis. Our findings provide a valuable tool for analysis of neural data, challenge simple categorization schemes previously proposed for these regions, and place useful constraints on neurocomputational models of economic choice and control. NEW & NOTEWORTHY We present a Bayesian method for formally detecting whether a population of neurons can be naturally classified into clusters based on their response tuning properties. We then examine several data sets of reward system neurons for variables and find in all cases that neurons can be classified into only two categories: a functional class and a non-task-driven class. These results provide important constraints for neural models of the reward system.

Keywords: clustering; functional subtypes; mixed selectivity; prefrontal cortex; reward.

Fig. 1.

Cartoon illustrating possible effects in a data set. Consider a set of neurons in which cells’ tuning properties for two parameters are independently assessed and then z-score transformed. Scatter plots are cartoon versions; each dot corresponds to a neuron; the two dimensions are two tuning dimensions. A: neurons may fall into pure-selectivity clusters. In the example, neurons are strongly tuned for parameter 1 or 2 but not both. B: another possibility is that neurons fall into a single larger cluster selective for both variables. In the presence of noise, it is often difficult to distinguish pure from multiple selectivity. C: a third possibility is that neurons will have no selectivity for either variable and will be best classified as nonselective. Some cells may be significantly tuned, but thus number is no greater than the false positive rate expected by chance. D: a population of neurons can also contain a combination of subsets that are pure and mixed, as for example when a population contains subpopulations correspond to each of two variables and a third that integrates them. E: neuronal populations can also contain other mixtures of these. In particular, our data suggest that a combination of multiple and no selectivity populations are common, perhaps even universal, in reward regions. F: conventional clustering methods make it difficult to judge categorical structure of populations. For example, a method like k-means clustering will divide cells into two categories (two blue ovals) even if they are from a single distribution.

Fig. 2.

Illustration of the approach used by our model. This visualization uses a simulated population with neurons coming from all three distributions. Fit distributions are colored based on which distribution they are most likely to have come from according to the model. Blue, multiple selectivity; green, pure tuning; red, no tuning. The row of three scatter plot panels shows the shape of each component of the model. The shading is proportional to the amount of weight on that component. Bottom panel shows the observed data, with the circles indicating the variance on the estimate of their location.

Fig. 3.

Illustration of the brain areas and tasks used in our data sets analyzed here.

Fig. 4.

Model fit to simulated data with correlated tunings. Model visualizations follow the same format as Fig. 2. A: model visualization for simulated data with a multiple tuned population with a 0.5 correlation between the tuning for X1 and X2. B: probability distribution functions of posteriors for A. C and D: same as A and B, but with a multiple and nonselective set. E and F: same as A and B, but with the population split between no tuning, pure tuning, and multiple tuning.

Fig. 5.

Weights converge quickly to correct answer as more data is given. Multiple selectivity (left) and no selectivity (right) weights for a multiple/no selectivity population (A), a pure/no selectivity population (B), and a multiple/pure/no selectivity population (C).

Fig. 6.

Model fit to orbitofrontal cortex (OFC) data set 1 (curiosity tradeoff task). A: we fit regression weights for reward sensitivity (x-axis) and informativeness (y-axis). Cells were categorized either as multiple tuning (blue oval) or as nonselective (red oval). B: posteriors. Most weight was put onto the multiple-tuning class, indicating neurons selectivity for both variables. The correlation between these variables was not found to be significant; it overlapped with zero. Pure selectivity signal weight applied to few cells. Data fit to no-tuning category shows a discrete cluster of cells that were not sensitive to either variable.

Fig. 7.

Summary of population data. Plots of weights given by the model to each of 20 neural data sets (see Fig. 7). Bars indicate credible intervals. A: weights given to multiple selectivity are high and overlap with 1.0 in all cases. B: weights given to pure selectivity are weak and overlap with zero in all cases. C: weights given to no selectivity are positive and do not include 0 in most cases.

Fig. 8.

Illustration of measured correlations and confidence intervals using standard methods (green bars) and using our methods described here. In all cases with significant effects, measured correlations were more extreme (farther from zero) using our method. Brain areas are indicated on the left as are references. Names of variables are indicated on the right. dACC, dorsal anterior cingulate cortex; vmPFC, ventromedial prefrontal cortex; VS, ventral striatum. References: (1) Strait et al. 2015; (2) Strait et al. 2014; (3) Wang and Hayden 2017; (4) Blanchard et al. 2015; (5) Strait et al. 2016; (6) Blanchard and Hayden 2014.