Dynamic prediction in functional concurrent regression with an application to child growth

Abstract

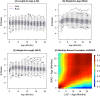
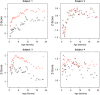
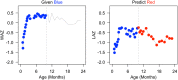
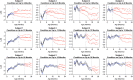
In many studies, it is of interest to predict the future trajectory of subjects based on their historical data, referred to as dynamic prediction. Mixed effects models have traditionally been used for dynamic prediction. However, the commonly used random intercept and slope model is often not sufficiently flexible for modeling subject-specific trajectories. In addition, there may be useful exposures/predictors of interest that are measured concurrently with the outcome, complicating dynamic prediction. To address these problems, we propose a dynamic functional concurrent regression model to handle the case where both the functional response and the functional predictors are irregularly measured. Currently, such a model cannot be fit by existing software. We apply the model to dynamically predict children's length conditional on prior length, weight, and baseline covariates. Inference on model parameters and subject-specific trajectories is conducted using the mixed effects representation of the proposed model. An extensive simulation study shows that the dynamic functional regression model provides more accurate estimation and inference than existing methods. Methods are supported by fast, flexible, open source software that uses heavily tested smoothing techniques.

Keywords: covariance function; fPCA; face; longitudinal data; mixed effects; penalized splines; sparse functional data.

Figure 1

Distribution of, A, length‐for‐age z‐scores (LAZ), B, weight‐for‐age z‐scores (WAZ), C, weight‐for‐length z‐scores (WLZ) binned into monthly categories, and, D, estimated empirical correlation between LAZ and WAZ at each month. Correlations were calculated using Z‐scores projected onto an evenly spaced grid of ages {0.5,1.5,…,23.5} for all subjects using face::face.sparse() applied separately to LAZ and WAZ

Figure 2

Length‐for‐age z‐score and weight‐for‐age z‐score curves for 4 children. Length‐for‐age z‐score is presented as ∘ and weight‐for‐age z‐score is presented as +

Figure 3

Illustration of dynamic prediction using a subject from the CONTENT study. Conditional on the weight‐for‐age z‐score (WAZ) and length‐for‐age z‐score (LAZ) data in blue, the interest is to predict the length‐for‐age z‐score (LAZ) in red

Figure 4

Estimated coefficient functions (solid lines) and associated 95% pointwise confidence intervals (dashed lines). WAZ, weight‐for‐age z‐score

Figure 5

Left to right: A, estimated correlation function; B, estimated variance function; C, first 5 estimated eigenfunctions (ϕ) and corresponding eigenvalues (λ)

Figure 6

Example of dynamic prediction for 4 subjects. Points represent subjects' observed length‐for‐age z‐score (LAZs), solid black/red lines represent the predicted curves, dashed black/red lines indicate 95% pointwise confidence intervals for the trajectories. Only observed data on and to the left of the vertical grey dashed line (blue points) are used for prediction