Machine learning unifies the modeling of materials and molecules

Abstract

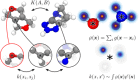
Determining the stability of molecules and condensed phases is the cornerstone of atomistic modeling, underpinning our understanding of chemical and materials properties and transformations. We show that a machine-learning model, based on a local description of chemical environments and Bayesian statistical learning, provides a unified framework to predict atomic-scale properties. It captures the quantum mechanical effects governing the complex surface reconstructions of silicon, predicts the stability of different classes of molecules with chemical accuracy, and distinguishes active and inactive protein ligands with more than 99% reliability. The universality and the systematic nature of our framework provide new insight into the potential energy surface of materials and molecules.

Fig. 1. SOAP-GAP predictions for silicon surfaces.

(A) The tilt angle of dimers on the reconstructed Si(100) surface [left, STM image (13); right, SOAP-GAP–relaxed structure] is the result of a Jahn-Teller distortion, predicted to be about 19° by DFT and SOAP-GAP. Empirical force fields show no tilt. (B) The Si(111)–7 × 7 reconstruction is an iconic example of the complex structures that can emerge from the interplay of different quantum mechanical effects [left, STM image (14); right, SOAP-GAP–relaxed structure colored by predicted local energy error when using a training set without adatoms]. (C) Reproducing this delicate balance and predicting that the 7 × 7 is the ground-state structure is one of the historical successes of DFT: a SOAP-based ML model is the only one that can describe this ordering, whereas widely used force fields incorrectly predict the unreconstructed surface (dashed lines) to a lower-energy state.

Fig. 2. SOAP-GAP predictions for a molecular database.

(A) Learning curves for the CC atomization energy of molecules in the GDB9 data set, using the average-kernel SOAP with a cutoff of 3 Å. Black lines correspond to using DFT geometries to predict CC energies for the DFT-optimized geometry. Using the DFT energies as a baseline and learning Δ_{DFT − CC} = E_CC − E_DFT lead to a fivefold reduction of the test error compared to learning CC energies directly as the target property (CC_DFT). The other curves correspond to using PM7-optimized geometries as the input to the prediction of CC energies of the DFT geometries. There is little improvement when learning the energy correction (Δ_{PM7 − CC}) compared to direct training on the CC energies (CC_PM7). However, using information on the structural discrepancy between PM7 and DFT geometries in the training set brings the prediction error down to 1 kcal/mol mean absolute error (MAE) (${\mathrm{\Delta }}_{\text{PM}7‐\text{CC}}^{\mathrm{\lambda }}$). (B) A sketch-map representation of the GDB9 (each gray point corresponding to one structure) highlights the importance of selecting training configurations to uniformly cover configuration space. The average prediction error for different portions of the map is markedly different when using a random selection (C) and FPS (D). The latter is much better behaved in the peripheral, poorly populated regions.

Fig. 3. Predictions of the stability of glucose conformers at different levels of theory.

(A) Extensive tests on 208 conformers of glucose (taking only 20 FPS samples for training) reveal the potential of an ML approach to bridge different levels of quantum chemistry; the diagonal of the plot shows the MAE resulting from direct training on each level of theory; the upper half shows the intrinsic difference between each pairs of models; the lower half shows the MAE for learning each correction. (B) The energy difference between three pairs of electronic structure methods, partitioned in atomic contributions based on a SOAP analysis and represented as a heat map. The molecule on the left represents the lowest-energy conformer of glucose in the data set, and the one on the right represents the highest-energy conformer.

Fig. 4. Predictions of ligand-receptor binding.

(A) ROCs of binary classifiers based on a SOAP kernel, applied to the prediction of the binding behavior of ligands and decoys taken from the DUD-E, trained on 60 examples. Each ROC corresponds to one specific protein receptor. The red curve is the average over the individual ROCs. The dashed line corresponds to receptor FGFR1, which contains inconsistent data in the latest version of the DUD-E. Inset: AUC performance measure as a function of the number of ligands used in the training, for the “best match”–SOAP kernel (MATCH) and average molecular SOAP kernel (AVG). (B and C) Visualization of binding moieties for adenosine receptor A2, as predicted for the crystal ligand (B), as well as two known ligands and one decoy (C). The contribution of an individual atomic environment to the classification is quantified by the contribution δz_i in signed distance z to the SVM decision boundary and visualized as a heat map projected on the SOAP neighbor density [images for all ligands and all receptors are accessible online (27)]. Regions with δz > 0 contain structural patterns expected to promote binding (see color scale and text). The snapshot in (B) indicates the position of the crystal ligand in the receptor pocket as obtained by x-ray crystallography (28). PDB, Protein Data Bank.

Fig. 5. A kernel function to compare solids and molecules can be built based on density overlap kernels between atom-centered environments.

Chemical variability is accounted for by building separate neighbor densities for each distinct element [see the study of De et al. (20) and the Supplementary Materials].