Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A Primer for parameter uncertainty, identifiability, and forecasts
- PMID: 29250607
- PMCID: PMC5726591
- DOI: 10.1016/j.idm.2017.08.001
Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A Primer for parameter uncertainty, identifiability, and forecasts
Abstract
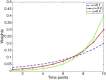
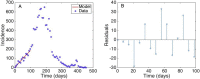
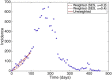
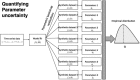
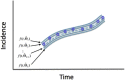
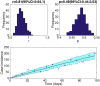
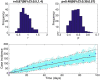
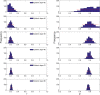
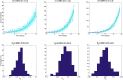
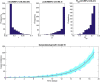
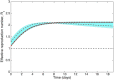
Mathematical models provide a quantitative framework with which scientists can assess hypotheses on the potential underlying mechanisms that explain patterns in the observed data at different spatial and temporal scales, generate estimates of key kinetic parameters, assess the impact of interventions, optimize the impact of control strategies, and generate forecasts. We review and illustrate a simple data assimilation framework for calibrating mathematical models based on ordinary differential equation models to time series data describing the temporal progression of case counts relating to population growth or infectious disease transmission dynamics. In contrast to Bayesian estimation approaches that always raise the question of how to set priors for the parameters, this frequentist approach relies on modeling the error structure in the data. We discuss issues related to parameter identifiability, uncertainty quantification and propagation as well as model performance and forecasts along examples based on phenomenological and mechanistic models parameterized using simulated and real datasets.
Keywords: Parameter estimation; bootstrap; forecasts; model performance; parameter identifiability; uncertainty propagation; uncertainty quantification.
Figures




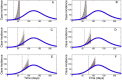
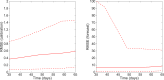

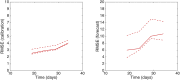
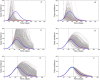
References
-
- Anderson R.M., May R.M. Directly transmitted infections diseases: Control by vaccination. Science. 1982;215(4536):1053–1060. - PubMed
-
- Anderson R.M., May R.M. Oxford University Press; , Oxford: 1991. Infectious diseases of humans.
-
- Arriola L., Hyman J.M. Sensitivity analysis for uncertainty quantification in mathematical models. In: Chowell G., editor. Mathematical and statistical estimation approaches in epidemiology. Springer Netherlands; 2009. pp. 195–247.
-
- Bailey N.T.J. Hafner; , New York: 1975. The mathematical theory of infectious disease and its applications.
-
- Banks H.T. An inverse problem statistical methodology summary. In: Chowell G., editor. Mathematical and statistical estimation approaches in epidemiology. 2009. pp. 249–302.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
