Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Dec 18;17(1):775.
doi: 10.1186/s12879-017-2874-y.

Mathematical models used to inform study design or surveillance systems in infectious diseases: a systematic review

Sereina A Herzog  1 , Stéphanie Blaizot  2 , Niel Hens  2   3
Affiliations

Mathematical models used to inform study design or surveillance systems in infectious diseases: a systematic review

Sereina A Herzog et al. BMC Infect Dis. .

Abstract

Background: Mathematical models offer the possibility to investigate the infectious disease dynamics over time and may help in informing design of studies. A systematic review was performed in order to determine to what extent mathematical models have been incorporated into the process of planning studies and hence inform study design for infectious diseases transmitted between humans and/or animals.

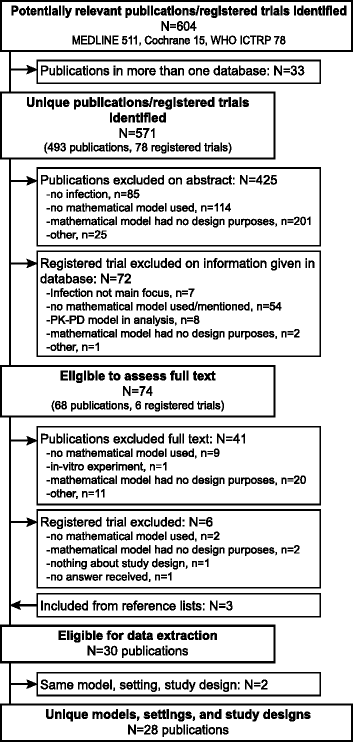
Methods: We searched Ovid Medline and two trial registry platforms (Cochrane, WHO) using search terms related to infection, mathematical model, and study design from the earliest dates to October 2016. Eligible publications and registered trials included mathematical models (compartmental, individual-based, or Markov) which were described and used to inform the design of infectious disease studies. We extracted information about the investigated infection, population, model characteristics, and study design.

Results: We identified 28 unique publications but no registered trials. Focusing on compartmental and individual-based models we found 12 observational/surveillance studies and 11 clinical trials. Infections studied were equally animal and human infectious diseases for the observational/surveillance studies, while all but one between humans for clinical trials. The mathematical models were used to inform, amongst other things, the required sample size (n = 16), the statistical power (n = 9), the frequency at which samples should be taken (n = 6), and from whom (n = 6).

Conclusions: Despite the fact that mathematical models have been advocated to be used at the planning stage of studies or surveillance systems, they are used scarcely. With only one exception, the publications described theoretical studies, hence, not being utilised in real studies.

Keywords: Infectious diseases; Mathematical models; Research design; Study design; Systematic review.

PubMed Disclaimer

Conflict of interest statement

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Figures

Fig. 1
Fig. 1
Flow diagram of included and excluded publications and registered trials
See this image and copyright information in PMC

References

    1. World Health Organization . Research for universal health coverage. Geneva, Switzerland: World Health Organization; 2013. - PubMed
    1. Anderson RM, May RM. Infectious diseases of humans: dynamics and control. Oxford, New York: Oxford University Press; 1991.
    1. Keeling MJ, Rohani P. Modeling infectious diseases in humans and animals. Princeton, NJ: Princeton University Press; 2008.
    1. Heesterbeek H, Anderson RM, Andreasen V, Bansal S, De Angelis D, Dye C, et al. Modeling infectious disease dynamics in the complex landscape of global health. Science. 2015;347:aaa4339. doi: 10.1126/science.aaa4339. - PMC - PubMed
    1. Garnett GP, Cousens S, Hallett TB, Steketee R, Walker N. Mathematical models in the evaluation of health programmes. Lancet. 2011;378:515–525. doi: 10.1016/S0140-6736(10)61505-X. - DOI - PubMed

Publication types